Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Układy wirujące, takie jak turbiny gazowe, są wykorzystywane do wytwarzania energii w przemyśle energetycznym lub napędu w przemyśle lotniczym i kosmicznym i są narażone na trudne warunki z wysokimi temperaturami i obciążeniami. W takich warunkach defekty powstałe podczas procesu produkcyjnego mogą mieć katastrofalny wpływ na działanie części. W przypadku braku równowagi w obciążeniu zewnętrznym lub gdy niedoskonałości wewnętrzne wpływają na symetrię układu, mogą wystąpić wibracje, które w zależności od prędkości obrotowej i charakterystyki wewnętrznej układu mogą uszkodzić część lub cały zespół. omówiliśmy to wcześniej na naszym blogu zatytułowanym -… Zapobieganie awariom silników lotniczych.
Odkształcenie termiczne (łuk termiczny) turbiny pojawia się w obecności pionowego gradientu temperatury, wywołanego procesem chłodzenia po wyłączeniu silnika. Po ponownym uruchomieniu silnika łuk wirnika może być odpowiedzialny za wysokie wibracje w silniku i musi być dokładnie zbadany. Łuk może być również spowodowany siłami statycznymi lub ciśnieniem.
W takim układzie możemy spodziewać się drgań, gdy konstrukcja odkształca się pod wpływem temperatury i obciążenia statycznego. ale drgania każdej obracającej się części mogą być również spowodowane jej niedoskonałościami, takimi jak mimośrodowość środka masy tarczy łopatkowej.
Ponadto wiele układów wirujących składa się z różnych elementów, które nie obracają się z tą samą prędkością. Na przykład w turbinie gazowej wysokociśnieniowe stopnie turbiny i sprężarki mogą obracać się trzy razy szybciej niż niskociśnieniowe stopnie turbiny i sprężarki. Musimy zatem zrozumieć, w jaki sposób wady zależne od prędkości obrotowej zostaną uwzględnione w odpowiedzi harmonicznej.
W tym wpisie na blogu zajmiemy się dwoma ważnymi scenariuszami odpowiedzi harmonicznej: niewyważeniem dynamicznym wywołanym przez odkształcony kształt (łuk termiczny) oraz wieloma niewyważeniami na różnych obracających się częściach.
Gdy odkształcenia termiczne i statyczne wywołują drgania obracającej się konstrukcji
Układy wirujące często doświadczają trudnych warunków temperatury, ciśnienia lub obciążeń, które mogą powodować drgania układu. We wcześniejszym artykule bloguprzedstawiliśmy, w jaki sposób na dynamikę mogą wpływać defekty wirnika spowodowane produkcją, takie jak nierównomierny rozkład masy lub niewspółosiowość wału. W tym blogu zobaczymy, jak warunki zewnętrzne powodujące deformację wirnika wpłyną na zachowanie wibracyjne układu.
Kształt łuku wywołany przez łuk termiczny deformuje strukturę, czyniąc ją asymetryczną względem osi wirnika. To odkształcenie przesuwa masę tak, że nie jest ona już równomiernie rozłożona wokół osi wirnika. Mimośrody względem osi wirnika wywołują niezrównoważone obciążenia, które są proporcjonalne do kwadratu prędkości obrotowej.
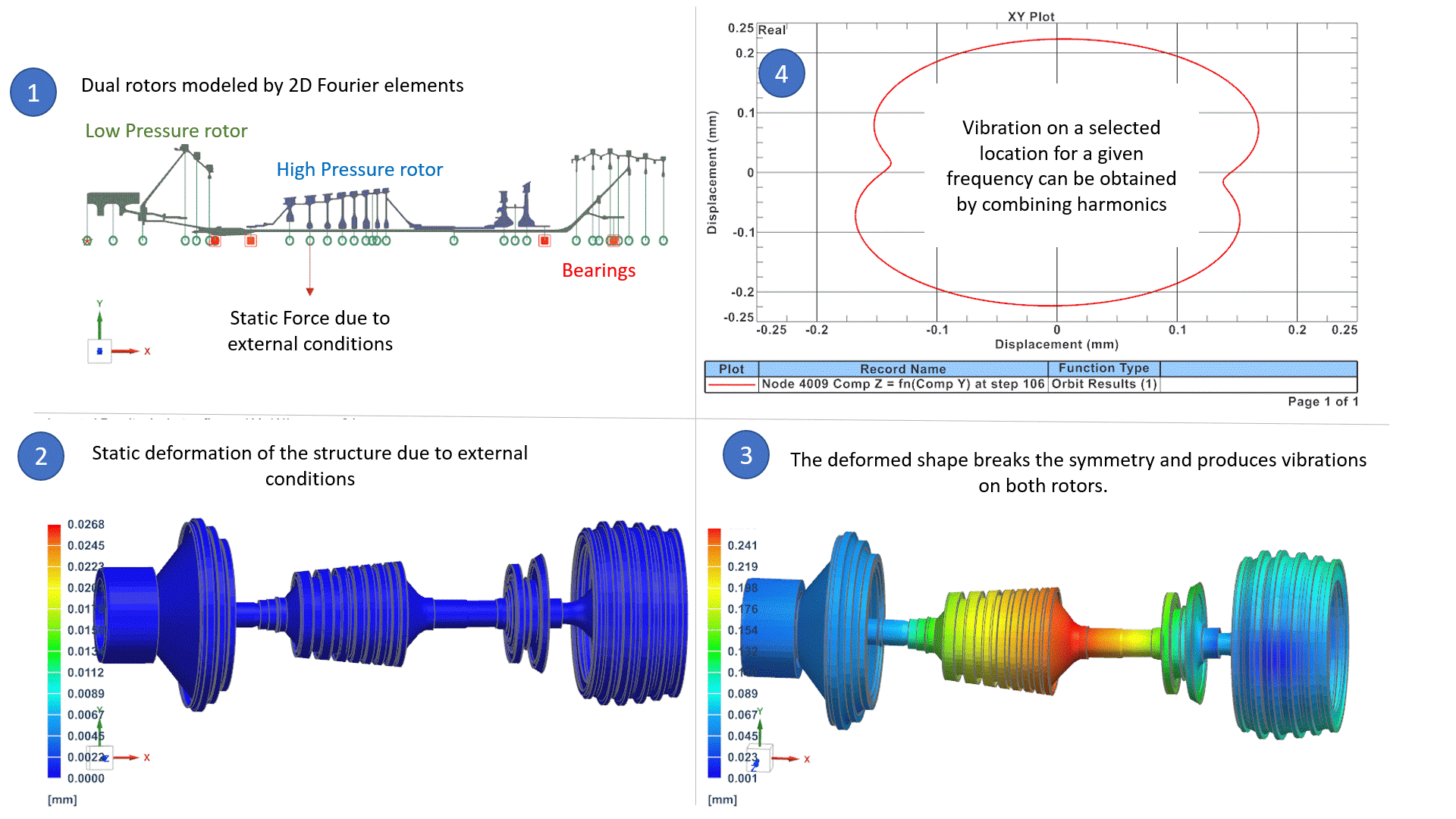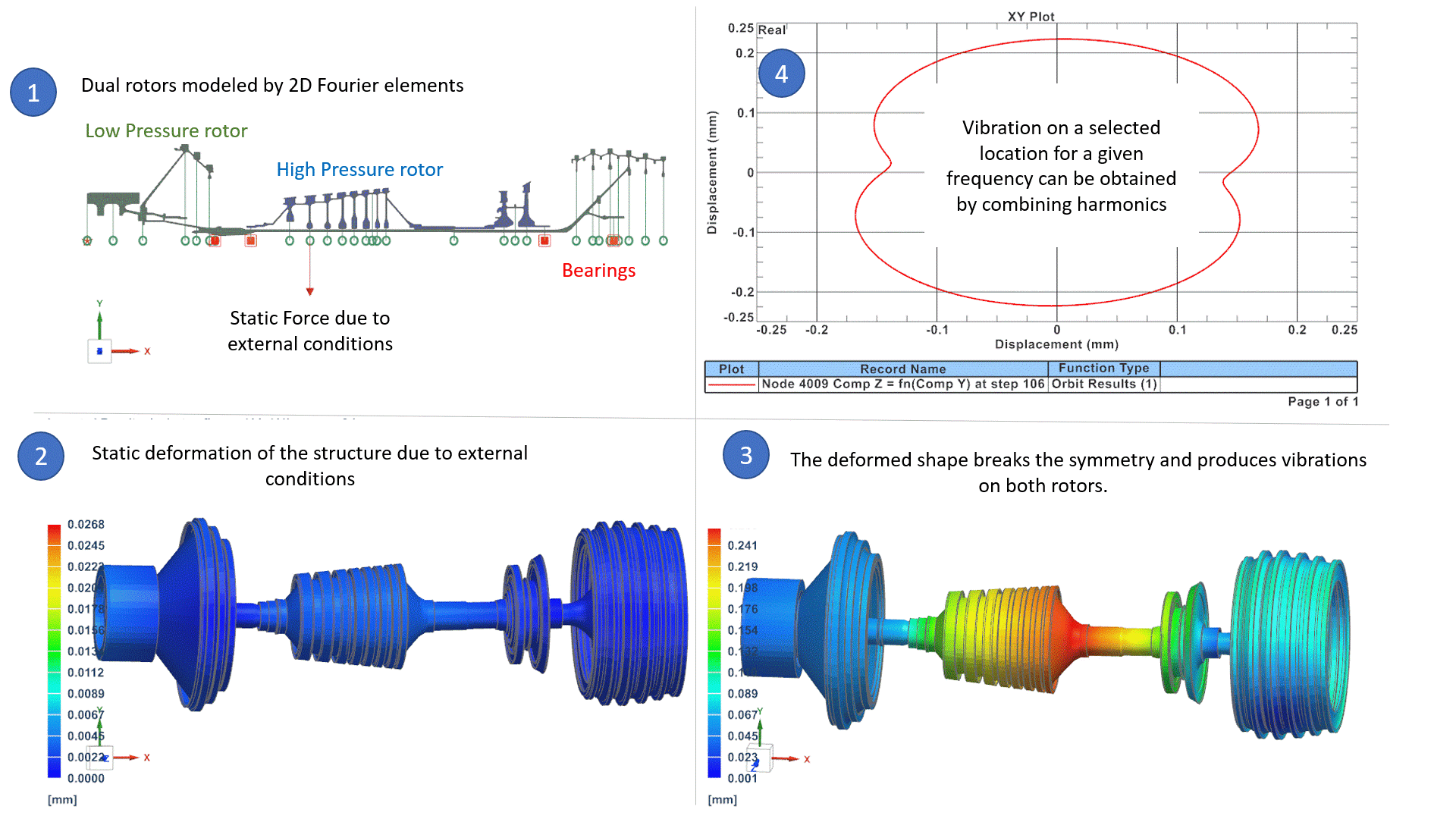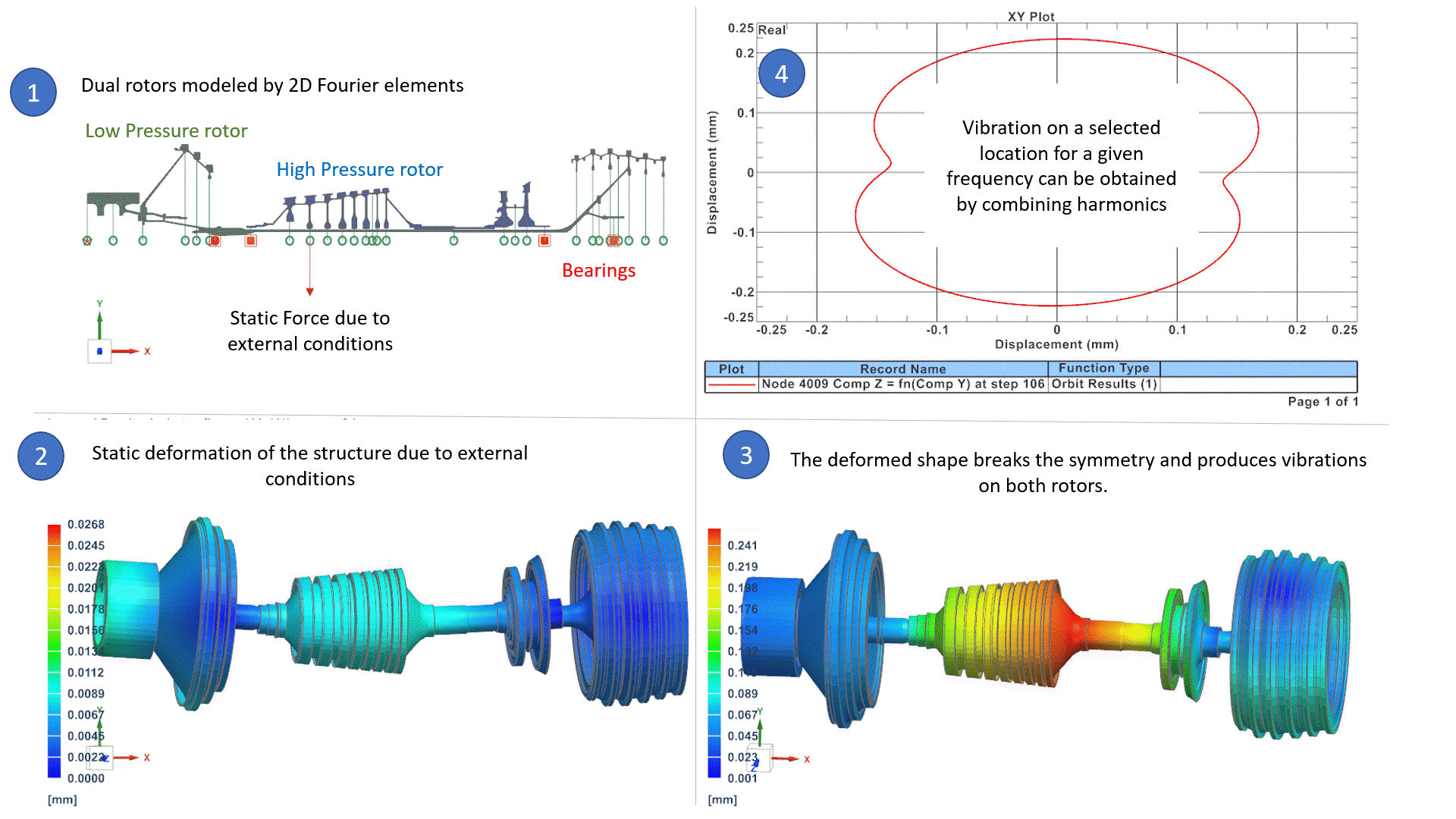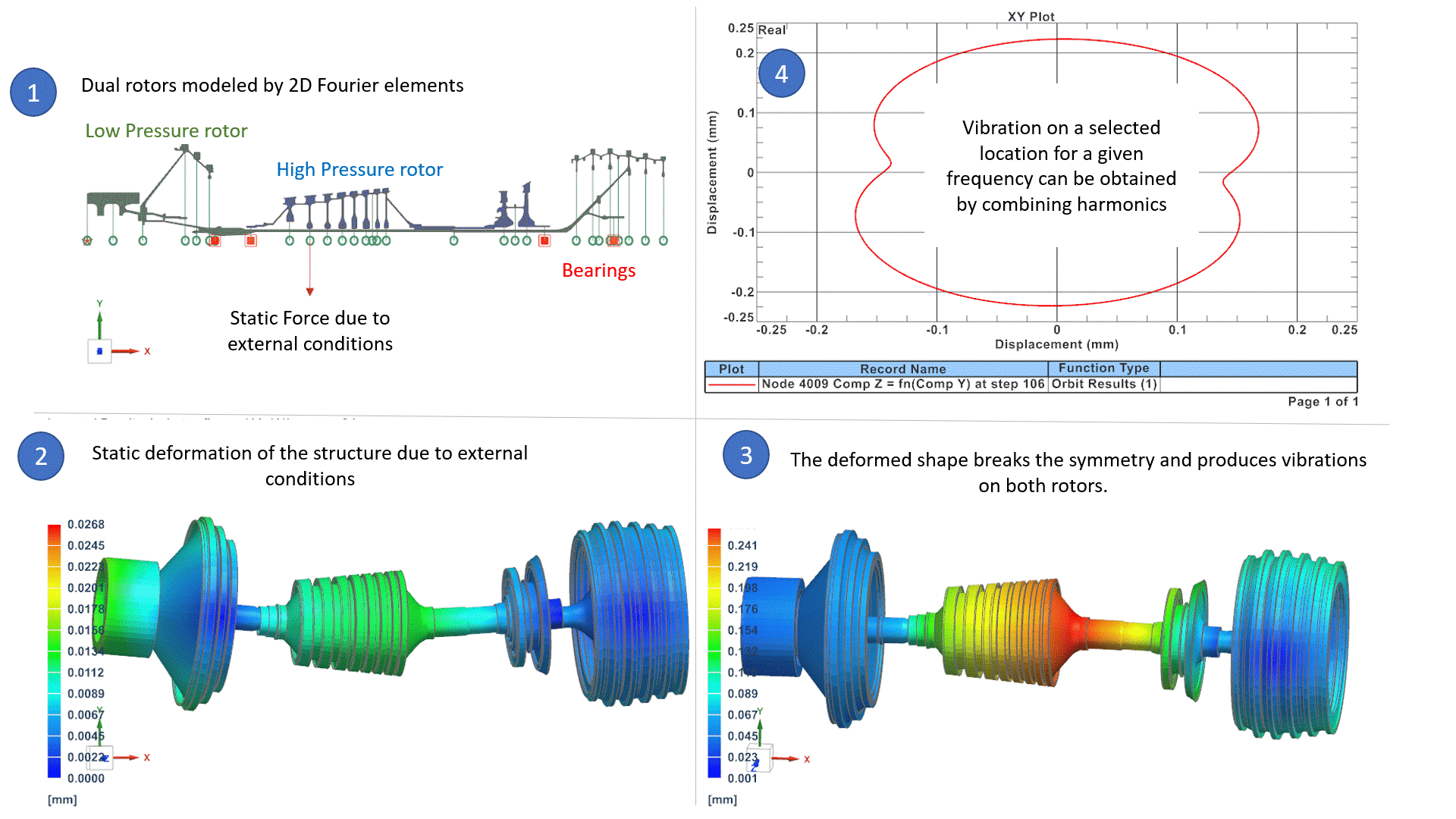
W powyższym przykładzie (1) system obrotowy składa się z dwóch wirników: wirnik wysokociśnieniowy obraca się 3 razy szybciej niż wirnik niskociśnieniowy. System jest modelowany za pomocą elementów Fouriera 2D (model osiowo-symetryczny z harmonicznymi Fouriera), co jest najlepszą alternatywą dla modeli 3D pod względem dokładności i czasu procesora, jak przedstawiliśmy we wcześniejszym artykule. Blog Post. Warunki zewnętrzne są takie, że siła statyczna odkształca wirniki w postaci łuku. (2) The kształt łuku łamie symetrię wirnika wokół osi obrotu. W konsekwencji, naturalnie indukuje to niewyważenie na obu wirnikach, które jest równe:
Masa x ecc x Ω2
Gdzie Ω jest prędkością wirnika każdy wirnik i ecc jest mimośrodowością wydedukowaną z odkształconego kształtu. Te niewyważenia na obu wirnikach powodują wibracje w całym systemie, które można badać w zakresach częstotliwości roboczych, aby upewnić się, że poziomy wibracji są akceptowalne. Wibracje są reprezentowane dla wybranej częstotliwości i wybranej harmonicznej w (3), a wykres orbitalny w (4) może odtworzyć całkowite wibracje systemu dla wybranej lokalizacji i częstotliwości. W dalszej części tego bloga omówimy, w jaki sposób oprogramowanie może zarządzać niezrównoważonymi obciążeniami, które odpowiadają różnym prędkościom obrotowym.
Niedoskonałości w obracających się częściach wywołują niepożądane obciążenia w obracającym się systemie
Początkowe defekty pochodzące z procesu produkcyjnego są niezależne od zewnętrznego obciążenia konstrukcji. Wywołują one jednak obciążenia w konstrukcji, które skutkują drganiami konstrukcji. Wśród typowych scenariuszy dynamiki wirnika, które wymagają testowania, symulacja niewyważonych defektów jest najwyższym priorytetem dla inżynierów. Wada niewyważenia występuje, gdy masa i środki geometryczne nie pokrywają się. Niewyważenie tworzy obciążenie, które jest wzmacniane wraz z prędkością obrotową wirnika Ω, proporcjonalnie do Ω2.

W poniższym klipie niewyważony system obrotowy zamontowany na elastycznych łożyskach może wykazywać bardzo wysokie amplitudy drgań, gdy system się obraca, szczególnie w przypadku niektórych prędkości obrotowych. Wartości szczytowe w odpowiedzi odpowiadają niepożądanym prędkościom krytycznym systemu. W wcześniejszym blogupokazaliśmy, jak zidentyfikować krytyczne prędkości systemu wykorzystującego rzeczywiste łożyska.
W zespole złożonym z wielu wirników obracających się z różnymi prędkościami może występować wiele niezrównoważonych defektów, z których każdy indukuje siły związane z różnymi prędkościami obrotowymi, a następnie różnymi częstotliwościami.
Badając odpowiedź harmoniczną, inżynierowie są zainteresowani zachowaniem systemu w jednym pełnym cyklu, w zakresie częstotliwości (lub prędkości obrotowych), jak omówiono wcześniej.
W przypadku pojedynczego defektu równanie ruchu jest rozwiązywane dla pojedynczej częstotliwości ω:

lub definiując dynamiczną macierz sztywności
Z(Ωω)q(ω)=g(ω)
Teraz, dla wielu defektów odpowiadających różnym prędkościom obrotowym, Simcenter 3D Rotor Dynamics używa wiele harmonicznych jednocześnie w celu rozwiązania symulacji. Każda harmoniczna odpowiada indywidualnej częstotliwości (prędkości obrotowej) każdego wirnika.
Równanie (5.1) staje się układem równań do rozwiązania dla różnych częstotliwości ω.
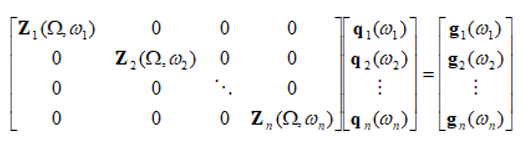
Równania układu nie są sprzężone, gdy wirniki są osiowo-symetryczne, więc cały zespół można rozwiązać w stałym układzie odniesienia, z zachowaniem łożysk reprezentowanym przez funkcje liniowe.
W symulacji wykorzystującej wiele harmonicznych, wyniki są wyprowadzane dla każdej indywidualnej harmonicznej ω1, ω2,… , co sprawia, że przetwarzanie końcowe jest mniej intuicyjne w porównaniu do przypadku monoharmonicznego.
Na szczęście możliwe jest ponowne połączenie wyników wszystkich harmonicznych w dziedzinie czasu poprzez wykresy orbitalne dla jednego lub kilku cykli w celu wyświetlenia wyniku końcowego.
W przykładzie podwójnych wirników, gdzie niewyważenia zostały wywnioskowane z odkształconego kształtu, dwie harmoniczne (ω1 i ω2) zastosowano zgodnie z dwiema prędkościami wirnika Ω1 dla wirnika niskociśnieniowego i Ω2=3Ω1 dla wirnika wysokociśnieniowego.
Dla każdej częstotliwości referencyjnej wynik przemieszczenia w kierunku Y dla harmonicznych ω1 i ω2 pokazano na poniższym rysunku.
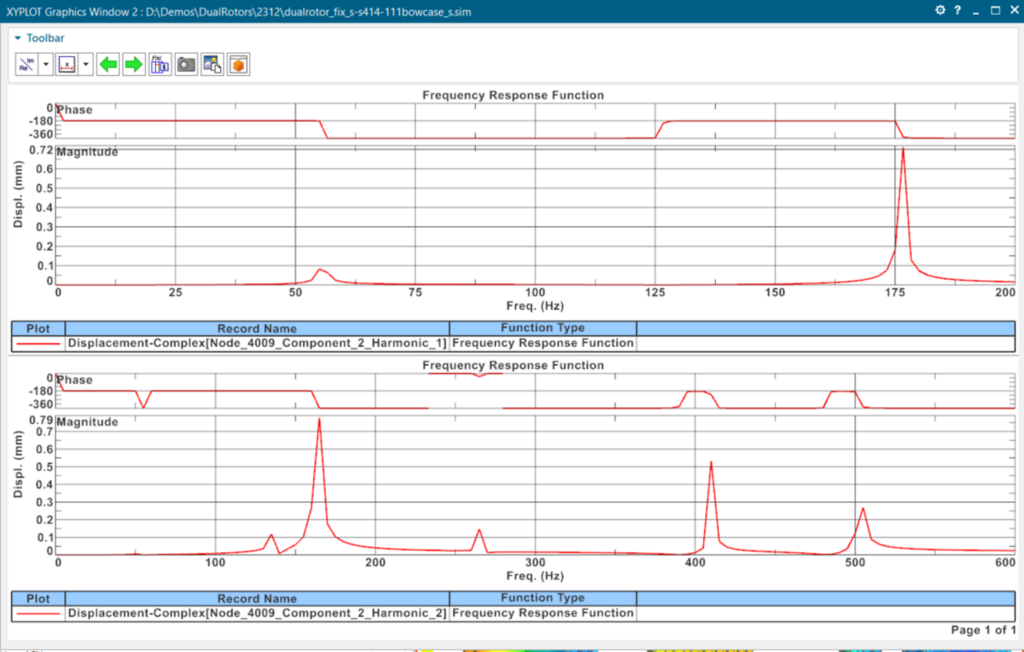
Po zidentyfikowaniu szczytu przemieszczeń przy ω1=55 Hz, możemy sprawdzić całkowite drgania, łącząc dwie harmoniczne dla przemieszczenia w kierunkach X i Y (prostopadle do osi wirnika):
X
Y
Gdzie (Xω1, Yω1) i (Xω2, Yω2) są drganiami obliczonymi odpowiednio w harmonicznej 1 i 2. Punkt na osi wirnika, który jest połączony z wirnikiem wysokociśnieniowym, można przedstawić za pomocą wykresu orbity (X
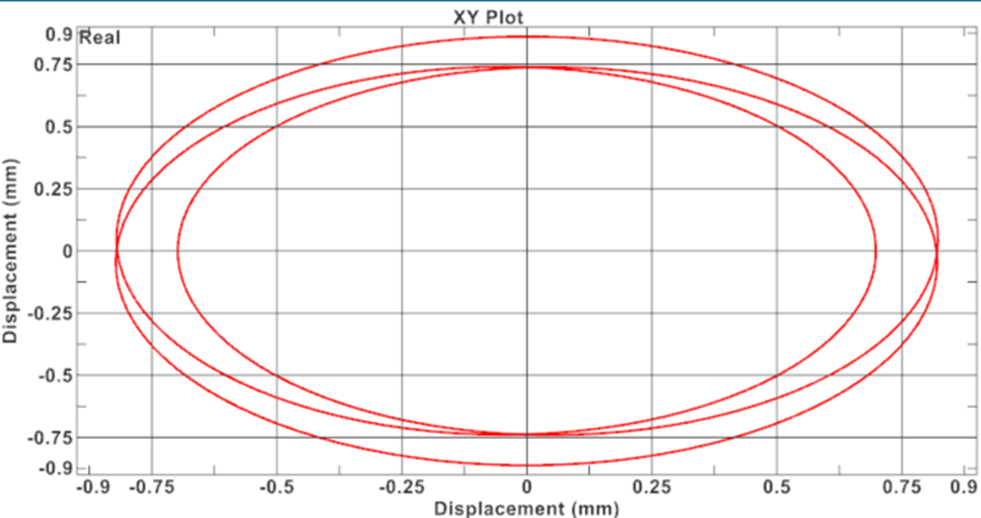
Dzięki takiemu wykresowi orbity inżynier może określić, czy wibracje w zakresie częstotliwości roboczych są dopuszczalne.
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.


