Zmniejszanie wymagań obliczeniowych w Abaqus za pomocą submodelowania

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.

Rozmiar i złożoność projektów produktów, które są analizowane i testowane za pomocą Abaqus – oprogramowania do analizy elementów skończonych (MES) i symulacji inżynierii wielu fizyk – stale rośnie. Submodelowanie jest skuteczną techniką, która może być stosowana, gdy wymagane są szczegółowe wyniki symulacji produktu dla małego, zlokalizowanego regionu w większym modelu, umożliwiając analitykowi znaczne zmniejszenie wymagań obliczeniowych i czasu wykonywania analizy.

Globalna analiza konstrukcji może być najpierw wykorzystana do zidentyfikowania obszarów, w których reakcja na obciążenie jest krytyczna. Następnie można utworzyć lokalny podmodel dla obszarów krytycznych, z ulepszoną reprezentacją geometryczną i/lub udoskonaleniem siatki. Ten lokalny podmodel zapewnia zwiększoną dokładność w stosunku do modelu globalnego bez konieczności ponownego siatkowania i ponownej analizy pełnego modelu. Takie podejście skutkuje zmniejszeniem kosztów analizy przy jednoczesnym zachowaniu wystarczającej szczegółowości w krytycznych regionach.

Na tym blogu przyjrzymy się teorii stojącej za submodelowaniem, dwóm technikom submodelowania dostępnym w Abaqus oraz sposobom implementacji submodeli. Podkreślimy również ograniczenia submodelowania w Abaqus i ważny etap weryfikacji wyników analizy.

Teoria submodelowania

Submodelowanie w Abaqus wykorzystuje zasadę Saint-Venanta, zgodnie z którą granica submodelu jest wystarczająco daleko od obszaru zainteresowania w submodelu, aby umożliwić zastąpienie przyłożonych sił równoważnymi siłami lokalnymi. Globalne rozwiązanie modelu jest wykorzystywane do zdefiniowania zachowania granicy podmodelu poprzez kontrolę zmiennych napędzanych, które są reprezentatywne dla przyłożonych sił. Rozwiązanie w obszarze zainteresowania nie jest zmieniane przez efekty końcowe, o ile obciążenia końcowe pozostają statycznie równoważne.

Na rysunku 1 przedstawiono przykład belki z kilkoma zlokalizowanymi otworami. Globalny model pełnej belki służy do określania zmiennych napędzanych jako danych wyjściowych na wspólnych granicach dla podmodelu i ułatwia użycie stosunkowo grubej siatki. Analizy są przeprowadzane niezależnie w modelu globalnym i podmodelu, a zmienne wymuszone są jedynym łącznikiem między nimi. Dzięki tej niezależności istnieje możliwość zmiany cech geometrycznych, typów elementów, właściwości materiałów itp. w celu poprawy reprezentacji podmodelowanego regionu. Podobnie jak w przypadku każdej techniki modelowania, ważne jest, aby zweryfikować wyniki, aby upewnić się, że są one fizycznie znaczące. Porównanie wykresu konturowego w pobliżu granic podmodelowanego obszaru modelu globalnego i podmodelu może być wykorzystane do potwierdzenia spójności wyników.

Techniki submodelowania w Abaqus

W programie Abaqus dostępne są dwie techniki submodelowania, określane jako submodelowanie oparte na węzłach i submodelowanie oparte na powierzchni. Technika oparta na węzłach interpoluje pole wyników węzłowych z modelu globalnego na węzły submodelu, jest to bardziej ogólna i powszechnie stosowana technika. I odwrotnie, w submodelowaniu powierzchniowym pole naprężeń jest interpolowane na punkty integracji powierzchni submodelu. Modelowanie podpowierzchniowe jest ograniczone do zastosowań typu bryła-ciało stałe i analizy statycznej, do wszystkich innych celów należy stosować modelowanie podpowierzchniowe oparte na węzłach. W zależności od atrybutów modelu, w analizie można zastosować dowolną z tych technik lub ich kombinację.

Technika oparta na powierzchni może zapewnić dokładniejsze wyniki naprężeń, jeśli w analizie statycznej występuje znaczna różnica w średniej sztywności w obszarze podmodelu, a model globalny podlega obciążeniu sterowanemu siłą. Natomiast gdy sztywność w regionach jest porównywalna, podmodelowanie oparte na węzłach zapewni podobne wyniki do podmodelowania opartego na powierzchni, przy zmniejszonym potencjale problemów numerycznych spowodowanych trybami sztywnego ciała. Różnice w sztywności mogą wynikać z dodatkowych szczegółów w podmodelu, takich jak otwory lub zaokrąglenia, lub z niewielkich zmian geometrycznych, które nie uzasadniają ponownego przeprowadzenia analizy globalnej.

Jeśli model jest poddawany dużym przemieszczeniom lub obrotom, podmodelowanie oparte na węzłach może poprawić dokładność podczas przesyłania dużych przemieszczeń i obrotów do podmodelu. W zależności od wyników wyjściowych, które są najbardziej interesujące. Modelowanie podrzędne oparte na węzłach zapewni dokładniejszą transmisję pola przemieszczenia w modelu podrzędnym. Natomiast modelowanie cząstkowe oparte na powierzchni zapewni dokładniejszą transmisję pola naprężeń, co skutkuje dokładniejszym określeniem sił reakcji w modelu cząstkowym. Te dwie techniki można uwzględnić w jednym modelu na różnych granicach.

Proszę wdrożyćing Abaqus Submodels

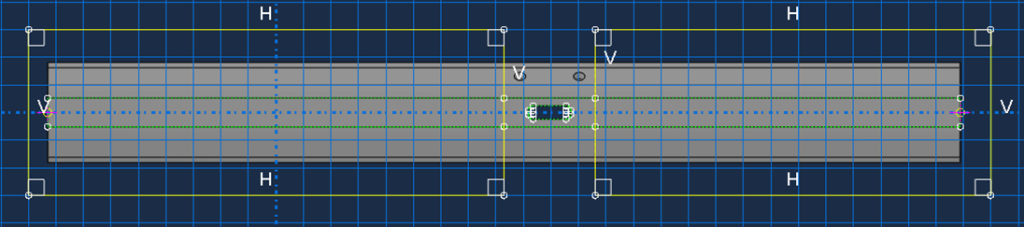
Model lokalny może być sterowany za pomocą danych zapisanych w pliku wyjściowej bazy danych (w formacie ODB lub SIM). Podmodele oparte na węzłach mogą być również sterowane za pomocą pliku wyników (.fil). Tylko zmienne zapisane w wyjściowej bazie danych będą używane w podmodelu, dlatego ważne jest, aby zapisywać odpowiednie dane wyjściowe z wystarczającą częstotliwością. Wyniki te muszą być zapisane w globalnym układzie współrzędnych w celu interpolacji na submodel. W przypadku danych węzłowych wartości są zawsze zapisywane w odniesieniu do kierunków globalnych do pliku wyjściowej bazy danych, niezależnie od tego, czy używane są transformacje współrzędnych węzłowych. Wszystkie napędzane zmienne powinny być zapisywane ze wspólną częstotliwością podczas globalnej analizy, a częstotliwość ta powinna być wystarczająco dokładna, aby umożliwić odpowiednie odtworzenie globalnej historii czasu dla napędzanych zmiennych. Jeśli wyniki są zapisywane z różnymi częstotliwościami, w analizie podmodelu zostanie użyta najgrubsza częstotliwość. Zaleca się utworzenie pojedynczego zestawu zawierającego wszystkie zestawy węzłów i/lub zestawy elementów, z których będzie sterowany submodel. Na rysunku 2 zestaw definiujący granicę submodelu jest podświetlony na czerwono i oznaczony jako Submodel-Region.

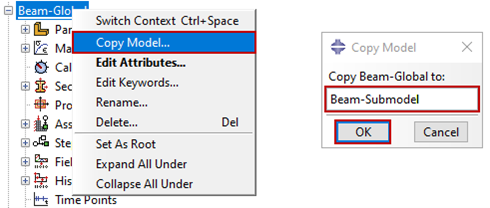
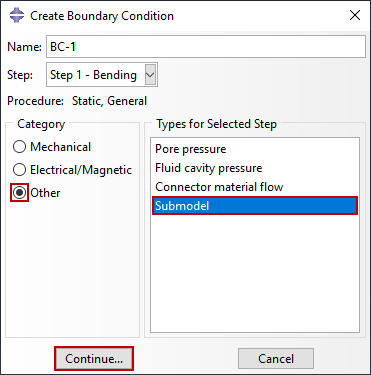
Do podmodelu można zastosować wszystkie rodzaje obciążeń i określone warunki brzegowe. Należy jednak zachować ostrożność, aby zastosować obciążenia i warunki brzegowe w podmodelu w sposób zgodny z modelem globalnym, aby uniknąć nieprawidłowych wyników. Tylko zmienne sterowane będą interpolowane i przenoszone do podmodelu. Wszelkie wstępnie zdefiniowane pola muszą być dostarczone tak, jak w modelu globalnym. Warunki początkowe powinny być spójne między modelem globalnym i podmodelem. Dla uproszczenia pomocne może być skopiowanie początkowego modelu globalnego w celu utworzenia modelu podrzędnego (Rysunek 3), przy użyciu narzędzi do tworzenia cięć w celu usunięcia materiału poza granicami modelu podrzędnego, jak pokazano na Rysunku 4. Takie podejście pozwoli na zachowanie ustawień modelu globalnego i zminimalizuje możliwość wystąpienia błędów podczas tworzenia modelu podrzędnego.

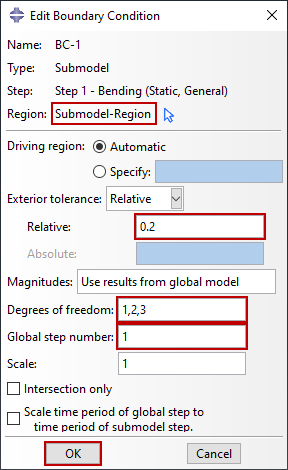
Czas kroku w analizie podmodelu powinien odpowiadać czasowi kroku w analizie globalnej, w przeciwnym razie jakakolwiek interpolacja w odniesieniu do czasu będzie nieprawidłowa. Jeśli występuje jakakolwiek rozbieżność, okres czasu globalnego kroku można przeskalować do tego w submodelu, przełączając opcję na Skaluj okres czasu kroku globalnego do okresu czasu kroku submodelu przy wdrażaniu warunków brzegowych pokazanych na rysunku 5.

Napędzane węzły są definiowane poprzez warunki brzegowe submodelu. Można określić, które stopnie swobody mają być napędzane na granicy submodelu – zazwyczaj określane są wszystkie stopnie swobody w napędzanych węzłach. Oprócz skalowania okresu czasu, Abaqus może skalować wartość zmiennych wymuszanych zastosowanych do podmodelu z modelu globalnego, gdy jest to właściwe. Na rysunku 5 zaimplementowano warunek brzegowy podmodelu, który obejmuje wszystkie stopnie swobody dostępne dla stałych elementów ciągłych (1-3) bez skalowania. Proszę zauważyć, że można sterować tylko podstawowymi zmiennymi rozwiązania. W submodelowaniu bryła-ciało stałe lub powłoka-powłoka obejmuje to przemieszczenia, temperatury, potencjał elektryczny, ciśnienie porowe itp. Prędkości lub przyspieszenia na granicy submodelu nie mogą być sterowane. Abaqus automatycznie wybiera napędzane zmienne, gdy globalny model powłoki jest używany do napędzania lokalnego modelu bryłowego. Inne warunki brzegowe submodelu mogą być tworzone, modyfikowane lub usuwane w zwykły sposób.

Abaqus interpoluje zarówno w przestrzeni, jak i w czasie, aby określić wartości napędzanych zmiennych węzłowych w całym kroku analizy submodelu. Kolejność interpolacji przestrzennej napędzanych zmiennych jest podyktowana kolejnością elementów używanych na poziomie globalnym. Automatyczna inkrementacja czasu jest stosowana niezależnie w analizach globalnych i podmodelowych. Niezależna inkrementacja czasu jest uwzględniana przez interpolację czasową zmiennych sterowanych. Liniowa interpolacja czasowa jest stosowana między wartościami odczytanymi z wyjściowej bazy danych lub pliku wyników.

Gdy model globalny podlega dużym przesunięciom lub obrotom, użytkownik musi upewnić się, że podmodel również podlega tym przesunięciom lub obrotom. Gdy używane jest modelowanie podrzędne oparte na węzłach, węzły sterujące automatycznie uwzględniają przemieszczenia i obroty, dzięki czemu model podrzędny będzie prawidłowo pozycjonowany względem globalnego układu współrzędnych. I odwrotnie, w przypadku podmodelowania opartego na powierzchni, użycie tylko trakcji powierzchniowych zapewnia podmodelowi brak informacji o przemieszczeniach. Zamiast tego, aby uwzględnić przemieszczenia, submodel musi zawierać: zastosowane warunki brzegowe, napędzane węzły i odciążenie bezwładnościowe. Gdy stosowane są obie metody, ważne jest utrzymanie spójnej metody prowadzenia w wybranym obszarze, aby zapobiec nadmiernym ograniczeniom wynikającym z częściowych lub nadmiernych definicji prowadzenia.

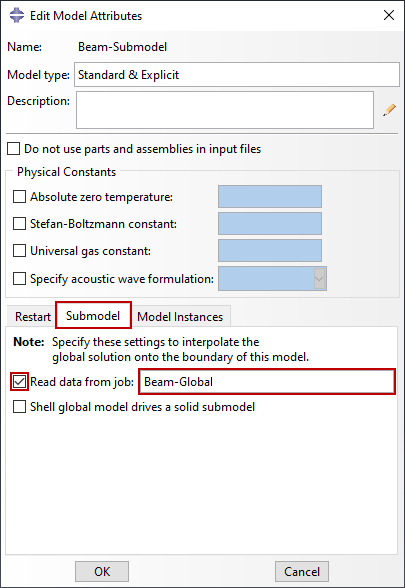
Podczas konfigurowania podmodelu atrybuty modelu należy zmodyfikować, aby odnosiły się do wyjściowej bazy danych lub pliku wyników. Atrybuty modelu pokazane na rysunku 6 spowodowałyby, że Abaqus odczytałby plik Beam-Global.odb i wykorzystać te wyniki w analizie podmodelu zdefiniowanego w pliku bazy danych wyjściowych. Beam-Submodel.inp plik wejściowy.

Ograniczenia submodelowania

Istnieją pewne ograniczenia dotyczące metod i typów elementów, które są zgodne z podejściem submodelowania. Ograniczenia zostaną pokrótce przedstawione tutaj, a więcej informacji na ich temat można znaleźć w dokumentacji.

Elementy, które mogą być używane na poziomie globalnym i podmodelu, są ograniczone do trójkątnych i czworokątnych elementów ciągłych, powłokowych lub membranowych pierwszego i drugiego rzędu, czworościennych, klinowych lub ceglanych elementów ciągłych pierwszego i drugiego rzędu. Modele globalne mogą zawierać zarówno elementy bryłowe, jak i powłokowe, z zastrzeżeniem, że wszystkie napędzane węzły muszą znajdować się wewnątrz elementów powłokowych w modelu globalnym.

Węzły graniczne podmodelu nie mogą znajdować się w regionach modelu globalnego, w których nie ma wystarczających informacji do interpolacji zmiennej wymuszonej. Obejmuje to regiony, w których znajdują się tylko elementy jednowymiarowe (takie jak belki, kratownice, łączniki lub powłoki osiowosymetryczne), elementy użytkownika, podkonstrukcje, sprężyny, punkty przyłożenia, inne elementy specjalne lub elementy osiowosymetryczne.

W przypadku korzystania z elementów powłokowych należy zazwyczaj unikać elementów powłokowych o pięciu stopniach swobody na węzeł (S4R5, S8R5 itp.) na poziomie globalnym, ponieważ obroty nie są zapisywane. Elementy te nie mogą być używane w podmodelowaniu powłoka-ciało stałe.

Podmodele nie mogą być używane w sprzężonych procedurach dynamiki liniowej termiczno-elektrycznej, termiczno-elektrochemicznej i opartej na modach. Podmodelowanie oparte na powierzchni może być używane tylko w ogólnych procedurach statycznych. Podmodelowanie typu shell-to-solid nie może być używane z żadnym innym typem podmodelowania w tym samym modelu.

Weryfikacja Wyniki analizy

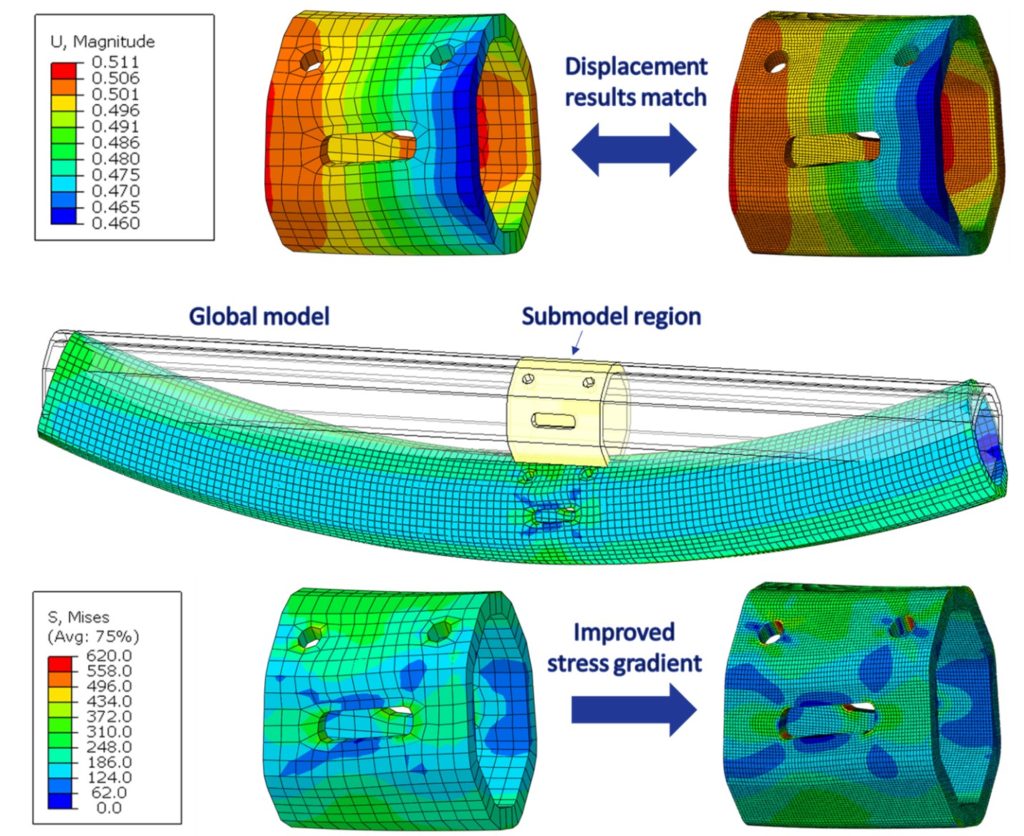
Podczas korzystania z podejścia submodelowania uzyskuje się następnie dwa zestawy wyników analizy: pierwszy z modelu globalnego dającego przybliżenie zachowania, a drugi z dopracowanego modelu lokalnego dającego bardziej precyzyjne odwzorowanie szczegółowych danych wyjściowych. Ważnym krokiem w procedurze submodelowania jest weryfikacja wyników. Na rysunku 7 przedstawiono wyniki submodelu opartego na węzłach. Model jest najpierw sprawdzany pod kątem spójności przemieszczeń w obszarze submodelu przed wykreśleniem gradientu naprężeń. Jeśli zidentyfikowane zostaną poważne rozbieżności w przemieszczeniach, wpłynie to na wszystkie kolejne wyniki, a model powinien zostać poddany przeglądowi i ponownie przesłany. Po stwierdzeniu zgodności przemieszczeń można sprawdzić inne dane wyjściowe, takie jak naprężenia. W tym przypadku poprawę gradientu naprężeń uzyskuje się poprzez zwiększenie gęstości siatki w podmodelowanym obszarze. Naprężenia w innych regionach belki można uzyskać z modelu globalnego, w którym przy braku otworów koncentrujących naprężenia, siatka zgrubna jest wystarczająca.

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.