Participe do fórum para Designers!
Sua experiência é vital para a comunidade. Junte-se a nós e contribua com seu conhecimento!
Participe do fórum agoraCompartilhe, aprenda e cresça com os melhores profissionais do setor.
Resumo
Na primeira parte desta série de discussões, explorei e verifiquei a relação entre os cálculos manuais e a resposta dependente do tempo de um objeto que está sendo lançado em uma superfície rígida e quais deflexões e tensões ocorrem durante esse período de impacto. Os conceitos discutidos abaixo são essenciais para a compreensão de como configurar e resolver uma análise estrutural transiente usando o ANSYS Mechanical.
Figura 1: Barra durante o impacto (com escala de deflexão exagerada).
A Figura 1 ilustra nossa barra de exemplo após ser derrubada e mostra o que acontece durante o período de impacto. O restante do documento explora como podemos configurar e analisar esse tipo de sistema e comparar nosso progresso com cálculos manuais comuns.
Aqui está uma lista dos tópicos abordados nesta discussão (em ordem de aparecimento):
- Energia potencial
- Energia Elástica
- Rigidez direcional
- Análise estrutural estática
- Força de compressão média
- Energia cinética
- Velocidade de impacto
- Período de impacto
- Frequência natural
- Massa efetiva modal
- Análise estrutural transitória
- Duração da análise
- Frequência do intervalo de tempo
- Resultados de tensão e deslocamento transiente complexo
- Tensão compressiva média
Detalhes
Comecei a explorar a relação entre os cálculos manuais e os resultados máximos de deflexão e tensão produzidos por eventos dinâmicos, como o impacto de um objeto em outro. Usei o ANSYS Mechanical como um meio de verificar as suposições e fornecer mais detalhes sobre esses eventos dinâmicos. Tenho fé no método de elementos finitos e estou ansioso para compartilhar minhas descobertas com os senhores.
Comecei minha exploração com um exemplo simples de uma barra cilíndrica sendo lançada em uma superfície rígida. Nesse cenário, e em todos os cenários associados a esta discussão, presumo que haja um comportamento elástico do material e que nenhuma das cargas causaria plasticidade ou danos. Isso significa que há conservação de energia dentro da geometria.
Durante esse processo, fiz uma série de suposições e realizei análises de elementos finitos para verificar ou contestar essas suposições. Esse processo me levou a fazer mais perguntas, analisar e obter mais respostas. No final, posso descrever com confiança muitos aspectos desse evento dinâmico, os quais apresentarei da forma mais concisa possível.
Vamos começar com a ideia mais simples.
Este primeiro exemplo explora a queda de uma barra cilíndrica em uma superfície rígida. A barra tem um diâmetro de 25,4 mm e um comprimento de 254 mm e densidade de massa de 7,85e-06 [kg/mm³]. Essa barra será lançada a 1 metro da face inferior.
Figura 2: Barra Cilíndrica
Sob essa circunstância, a energia potencial deve ser igual à energia elástica.
Energia potencial:

Energia elástica:

Vamos equiparar a energia potencial de nosso cilindro em queda com sua energia elástica para saber se podemos prever as deflexões com precisão.
Vamos supor que a barra será lançada de forma que se desloque na direção Y negativa. Portanto, a primeira etapa será determinar a rigidez de nossa geometria na direção Y.
Para o nosso modelo, essa rigidez pode ser derivada teoricamente, bem como pelo uso do método de elementos finitos, aplicando uma carga conhecida e dividindo essa carga pela deflexão calculada na direção Y. Isso nos permitirá comparar os resultados de nossa estimativa de elementos finitos com o valor derivado teoricamente e desenvolver confiança em nossa metodologia.
Vamos derivar nossa rigidez teórica. Para a direção Y, a seguinte fórmula será aplicada:

Agora, vamos calcular também a rigidez da geometria por meio de uma análise de elementos finitos por dois métodos diferentes, para que possamos entender as diferentes considerações envolvidas com diferentes tipos de cargas.
Aqui, consideramos uma base fixa enquanto aplicamos uma força à extremidade distal do nosso cilindro, de modo que a força de reação na base seja igual em magnitude e de sinal oposto à força aplicada na parte superior do cilindro. A magnitude dessa carga compressiva não é crítica, desde que as propriedades do nosso material sejam lineares e que não estejamos considerando a não linearidade da geometria (grande deformação).
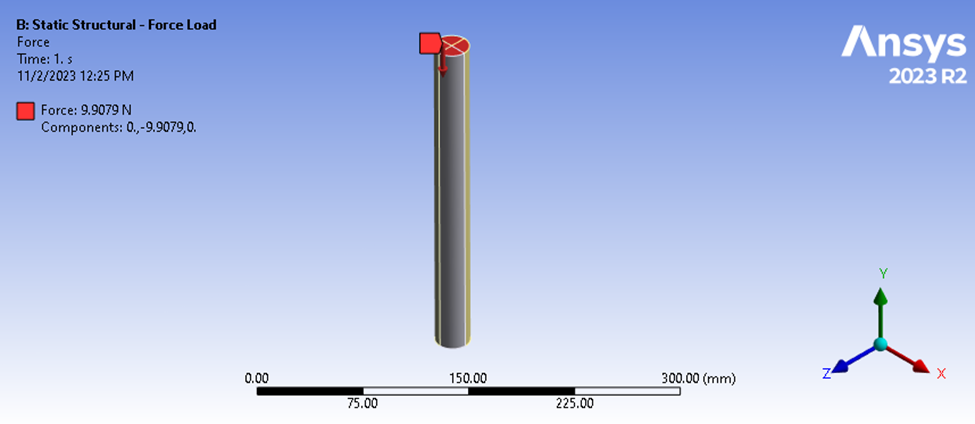
Figura 3: Análise estrutural estática da haste carregada pela parte superior e apoiada na parte inferior.
Nesse cenário, uma carga de 9,9079 N é aplicada à superfície superior enquanto a superfície inferior é fixada a partir de deslocamentos Y. A magnitude dessa carga ficará mais clara posteriormente.
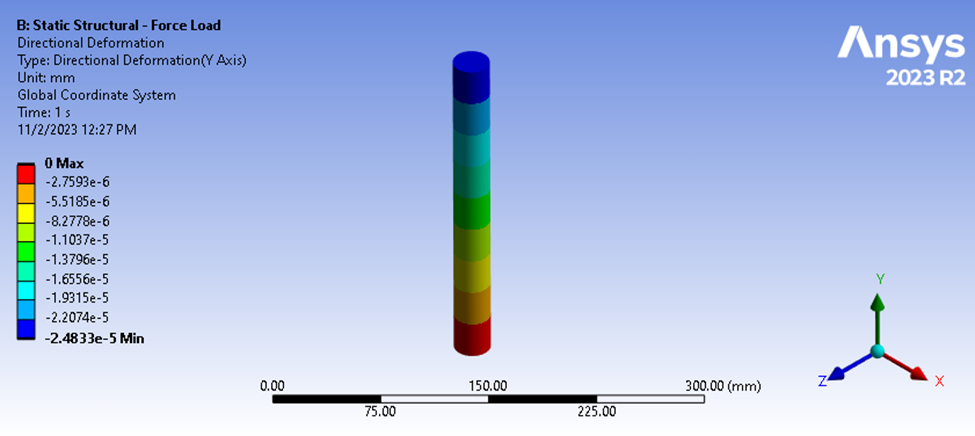
Figura 4: Resultados da deflexão estrutural estática
A solução da análise estrutural estática mostra uma magnitude máxima para nossa deflexão compressiva de 2,4833e-5 mm. Com base em nossa carga de 9,9079 N, podemos calcular a seguinte rigidez média.
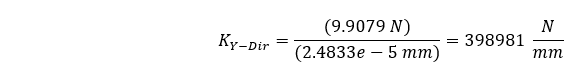
Pode-se ver que a abordagem de elementos finitos demonstra apenas 0,00125% de diferença em relação à abordagem teórica. Isso nos faz sentir bem 😊
Em seguida, vamos considerar um tipo diferente de carregamento, como o carregamento por gravidade. Aqui, a força é removida da superfície superior, mas a superfície inferior permanece restrita, e a gravidade é aplicada a 9806,6 mm/seg^2. A força de reação na base é de 9,9079 N, mas a força que atua na superfície superior é definitivamente zero. Os resultados da deflexão mostram uma magnitude de deflexão diferente de 1,2421e-5 mm.
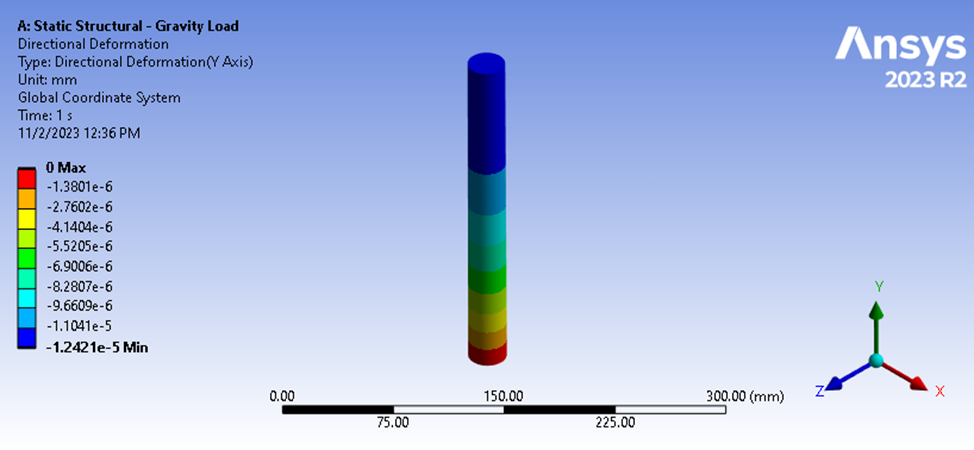
Figura 5: Resultados da deflexão da análise estrutural estática
Se tentássemos calcular a rigidez pela mesma forma da equação acima, chegaríamos a um valor incorreto porque não estaríamos considerando a força compressiva média que atua em nossa geometria. Nesse caso, nossa força de compressão média pode ser estimada facilmente, pois nossa geometria tem uma seção transversal constante e nossa rigidez média estimada pode ser calculada da seguinte forma.
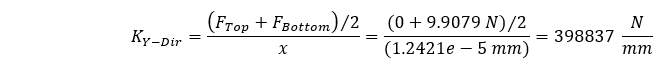
Essa estimativa demonstra uma diferença de 0,0348% em relação ao nosso valor calculado teoricamente. Portanto, por meio de dois métodos de carregamento diferentes, podemos estimar com segurança a rigidez da direção da geometria.
Substituindo nossa rigidez direcional estimada, juntamente com nosso modelo e propriedades do material, podemos estimar nossa deflexão máxima abaixo.
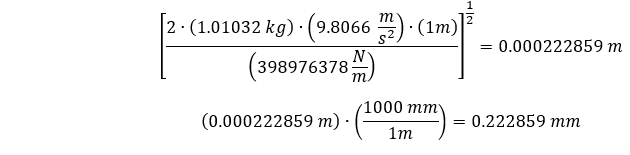
Que é cerca de ~0,223 mm. Agora precisamos de um modelo estrutural transitório para simular as deflexões no momento e após o momento do impacto de nossa barra cilíndrica com o solo.

Figura 6: Modelo de análise estrutural transitória e restrições
Nosso modelo supõe que a barra esteja se movendo a 4.428 mm/s na direção Y negativa. Essa é a velocidade que a barra atingiria se caísse 1 m. Podemos calcular isso igualando a energia potencial do eixo à sua energia cinética no momento do impacto.
Energia cinética:
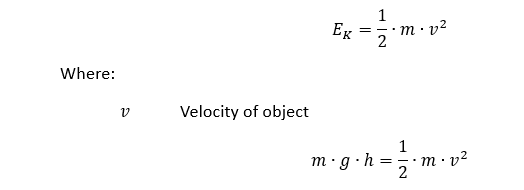
Portanto:

As restrições são adicionadas para manter a estatura vertical da geometria, enquanto um suporte somente de compressão é adicionado à base. A duração da análise é definida (mais sobre isso posteriormente), juntamente com uma taxa de captura frequente para a coleta de resultados.
Os resultados da análise são complicados, pois como a parte superior da barra está se desviando para baixo após o impacto, a parte inferior da barra pode ser ligeiramente comprimida devido à rigidez associada ao suporte somente de compressão. É a diferença na deflexão entre essas duas superfícies que descreve a compressão geral da barra.
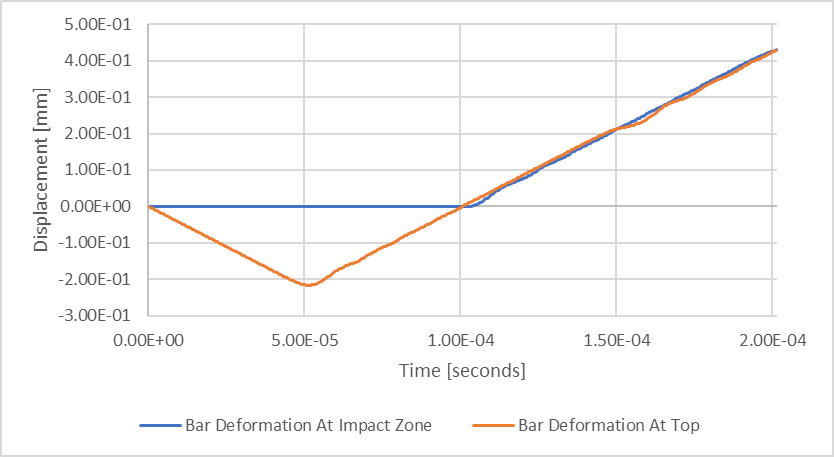
Figura 7: Resultados da deflexão estrutural transitória
O período plano da linha azul, “Bar Deformation at Impact Zone” (Deformação da barra na zona de impacto), demonstra o período em que ocorre o contato na base, ou a permanência associada ao impacto. Se replotarmos nossos dados para nos concentrarmos nesse período, poderemos fazer várias observações com mais facilidade.
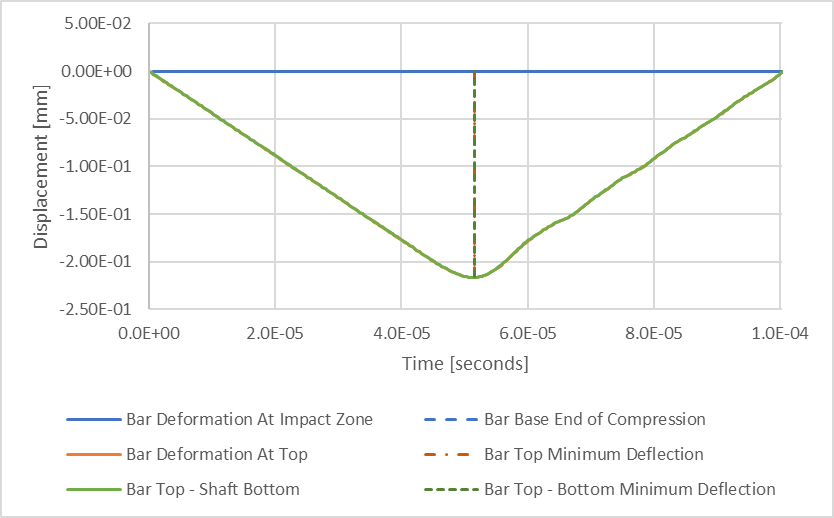
Figura 8: Resultados da deflexão compressiva estrutural transiente
Acrescentei uma linha verde que representa a diferença entre as deflexões das superfícies superior e inferior da barra, resultando na compressão total da barra em função do tempo. As duas linhas tracejadas verticais representam os intervalos de tempo associados aos resultados mínimos das linhas laranja e verde. É possível observar que a compressão mínima da barra ocorre ao mesmo tempo que a compressão mínima da parte superior da barra. A partir disso, podemos estimar que a compressão máxima de nossa barra é de 0,216 mm, o que é pouco menos de 3% menor do que a deflexão máxima estimada de 0,223 mm.
No entanto, há mais a ser explorado e aprendido com esse exemplo e seus resultados.
Vamos agora abordar o aspecto da configuração de uma análise estrutural transitória e, especificamente, abordar o período de tempo associado ao nosso evento e determinar como podemos estimar esse período para qualquer geometria.
Se observarmos o momento em que a linha azul passou do deslocamento negativo para o deslocamento positivo (0,00010026 segundos), o que equivale ao período associado à compressão do nosso eixo.
Nosso eixo pode ser considerado uma mola que salta. A duração do impacto é reflexo de ½ do período de sua frequência natural na direção da compressão. Portanto, o seguinte deve ser verdadeiro.

Agora vamos explorar se podemos apoiar essa teoria e como podemos estimar a frequência natural para essa e qualquer geometria que esperamos analisar no futuro.
Podemos alterar o suporte de “somente compressão” aplicado ao modelo de teste acima, com uma restrição de direção Y nessas mesmas superfícies e resolver diretamente nossa frequência de vibração longitudinal no ANSYS.
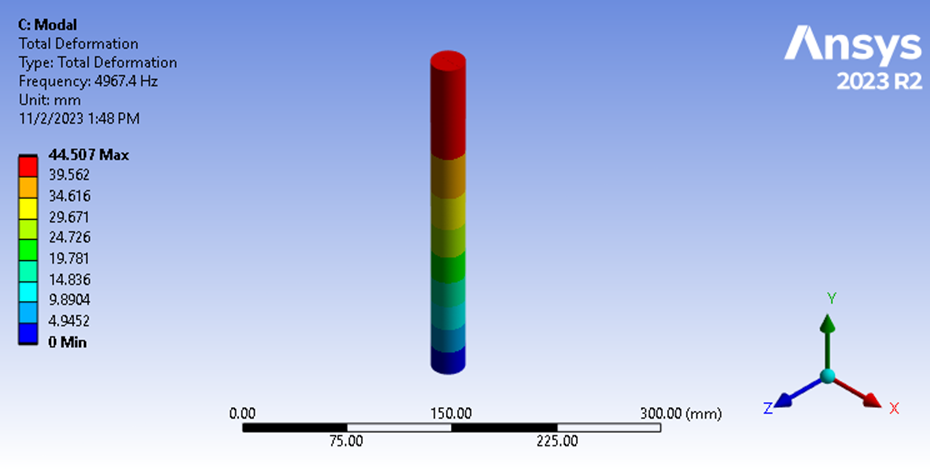
Figura 9: Frequência fundamental da análise modal
Aqui vemos que a frequência de vibração longitudinal é de 4967,4 Hz. Isso mostra que nossa estimativa da frequência natural com base em nossos resultados de deslocamento estrutural transitório foi precisa, com precisão de 0,4%. Essa constatação confirma nossa teoria de que a duração do impacto é igual a ½ do período da frequência fundamental para o sofá de dois objetos em impacto.
Figura 10: Período de impacto
Em nossa análise de exemplo, temos apenas uma parte e presumimos que o suporte vertical somente de compressão representa outro objeto muito rígido. Portanto, nosso eixo é o mais flexível desses dois parceiros de impacto. Nossa análise estrutural transitória foi definida para ter uma duração de análise igual ao período dessa frequência natural, e esperamos que o impacto ocorra durante a primeira ½ desse período.
Mas como calcular essa frequência natural se estivermos configurando uma análise estrutural transitória?
Podemos fazer o que acabei de demonstrar, ou seja, realizar uma análise modal da geometria e, ao mesmo tempo, usar restrições para manter a postura de impacto e resolver diretamente a forma modal da compressão de impacto. Mas existe uma maneira analítica de realizar a mesma coisa?
Para explorar isso, precisamos calcular a frequência natural da nossa geometria na direção do impacto, que pode ser calculada da seguinte forma.

Já exploramos como podemos estimar a rigidez direcional, mas agora vamos considerar alguns exemplos para entender melhor a consideração da massa efetiva modal.
A massa total do nosso sistema é:
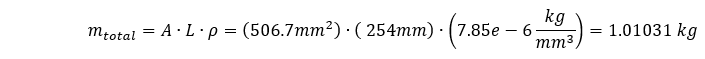
A massa efetiva do nosso sistema será menor do que a massa total, pois uma extremidade da nossa geometria é restrita. Pode ser difícil estimar a quantidade de massa que participará com base na complexidade de nossa geometria e nas restrições usadas para fixar a geometria. No nosso caso, a geometria é simples e, para seções transversais extrudadas que são fixadas em uma extremidade, a massa efetiva é geralmente derivada como sendo igual a 1/3 da massa total do sistema. Se esse fosse o caso, então a frequência fundamental seria a seguinte:
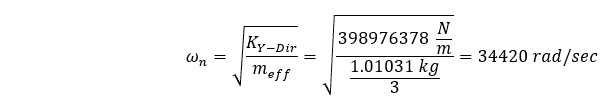
O que pode ser mais reconhecidamente declarado como:
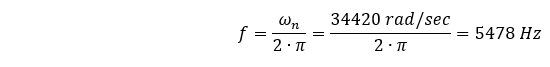
Esse valor (5478 Hz) é mais de 10% maior do que nossa frequência natural (4967,4 Hz) calculada pelo método de elementos finitos… por quê?
A resposta está relacionada à estimativa da massa efetiva modal. Se estivermos confiantes no cálculo da rigidez longitudinal (…estamos confiantes…), poderemos alterar a configuração do nosso modelo para verificar mais facilmente o cálculo da nossa frequência fundamental.
Vamos definir a densidade de massa do nosso material para o nosso modelo igual a zero e, em seguida, adicionar 1,01031 kg de massa à extremidade distal da nossa geometria, o que deve produzir a seguinte frequência natural.
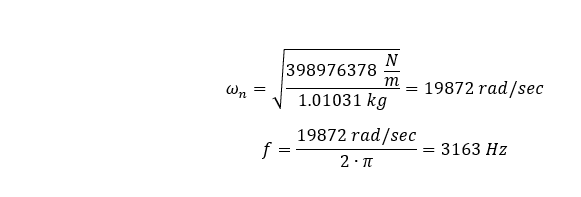
Depois de executar a análise de elementos finitos, vemos que a frequência longitudinal fundamental é de 3154,6 Hz.
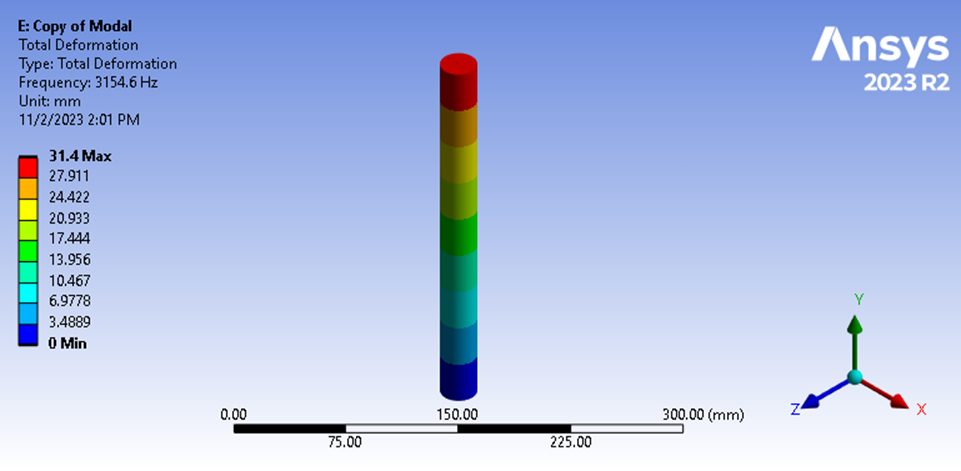
Figura 11: Frequência fundamental da análise modal
Isso reflete uma diferença de 0,27% em relação ao nosso cálculo manual. Portanto, desenvolvemos mais confiança no método de elementos finitos e identificamos um ponto fraco em nossa estimativa da massa efetiva usada em nosso cálculo manual, utilizando a massa distribuída em toda a nossa geometria.
Ao reorganizar nossa equação, podemos resolver essa massa efetiva considerando a frequência natural calculada pelo ANSYS ao considerar a massa distribuída da seguinte forma:
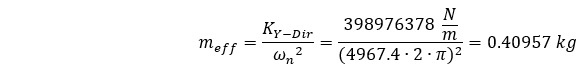
Descobrimos que essa massa efetiva é 0,405 da massa total do sistema.
Portanto, para outras geometrias mais complexas, podemos esperar que essa fração de massa seja única e desafiadora para derivar teoricamente e que possamos resolver de forma confiável a frequência natural usando o método de elementos finitos.
Agora que entendemos como determinaremos a frequência natural para uma determinada geometria, precisamos determinar em que frequência devemos coletar os resultados da análise durante nossa análise transitória.
Para fazer isso, devemos considerar como o tamanho da etapa de análise afeta a análise de duas perspectivas diferentes. Uma perspectiva é em termos do que se poderia esperar usando uma caracterização linear por partes de uma resposta não linear, como uma onda senoidal. A outra perspectiva está relacionada a como os resultados reais da análise mudam em função da mudança na frequência da taxa de captura. Como estamos considerando um problema de impacto e assumimos que o período de impacto está associado à vibração fundamental do nosso componente flexível, faz sentido explorar a relação entre o tamanho do passo e como isso afeta a precisão que representa uma curva senoidal.
Para avaliar essa relação, compararemos a média ponderada da magnitude da primeira metade da curva senoidal com a média teórica desse mesmo intervalo, que é igual a
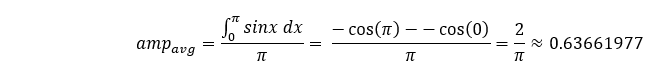
Agora vamos explorar a precisão com que, usando um número diferente de etapas, representamos essa curva senoidal e, em seguida, usaremos a regra trapezoidal para calcular a área sob a curva para a primeira metade e, depois, dividiremos essa área pelo período desse intervalo.
Figura 12: 4 etapas; média ponderada estimada=0,5; diferença de 21,46%
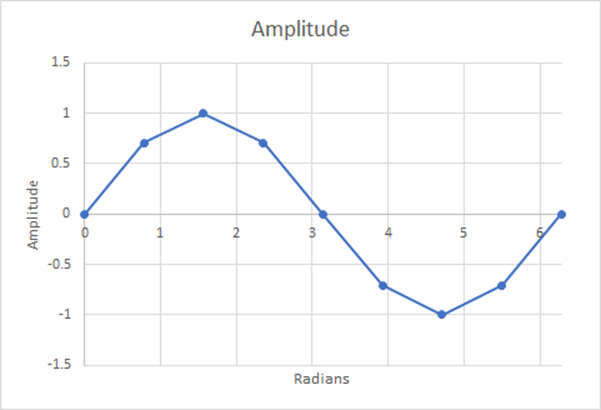
Figura 13: 8 etapas; média ponderada estimada=0,60536; diferença de 5,19%
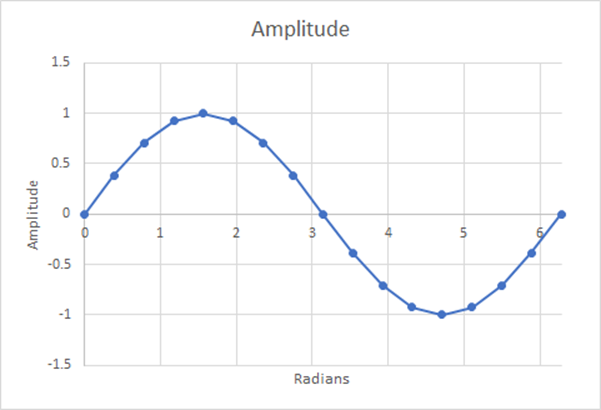
Figura 14: 16 etapas; média ponderada estimada=0,6284; diferença de 1,29%
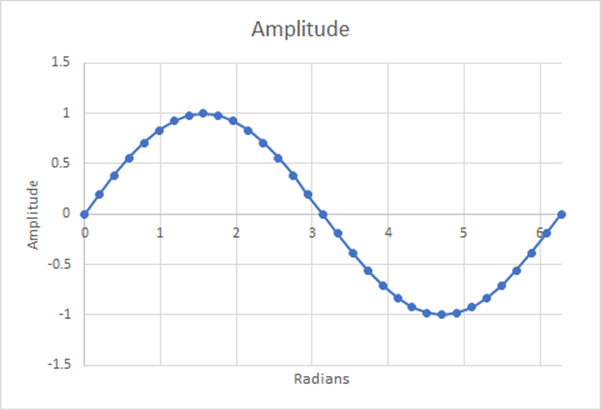
Figura 15: 32 etapas; média ponderada estimada=0,6346; diferença de 0,32%
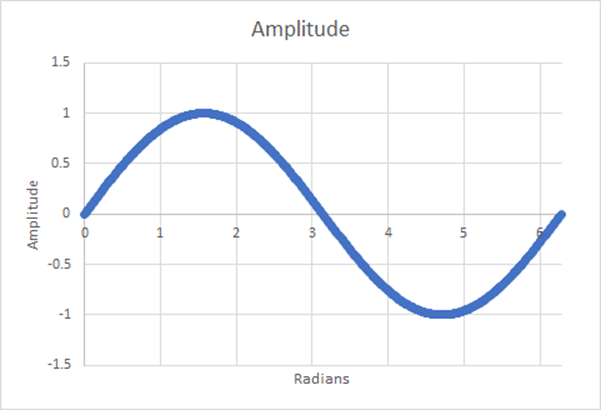
Figura 16: 512 etapas; média ponderada estimada=0,6366; diferença de 0,001%
Na verdade, nunca chegamos a uma concordância perfeita com o valor teórico, e podemos traçar um gráfico de como essa precisão muda à medida que o número de etapas de tempo aumenta, conforme ilustrado abaixo.
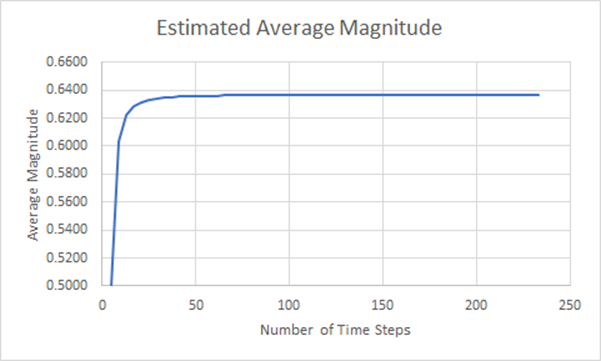
Figura 17: Gráfico de convergência da magnitude média estimada
A partir desse exame, podemos ver que grandes aumentos na precisão ocorrem rapidamente à medida que aumentamos o número de etapas em nossa aproximação. Mas isso não leva em consideração como os resultados se desenvolvem à medida que o número de etapas de tempo é aumentado.
Para explorar a influência nos resultados da análise, plotaremos nossos resultados de compressão máxima da haste em função do tempo, considerando diferentes números de etapas de tempo definidas na solução.
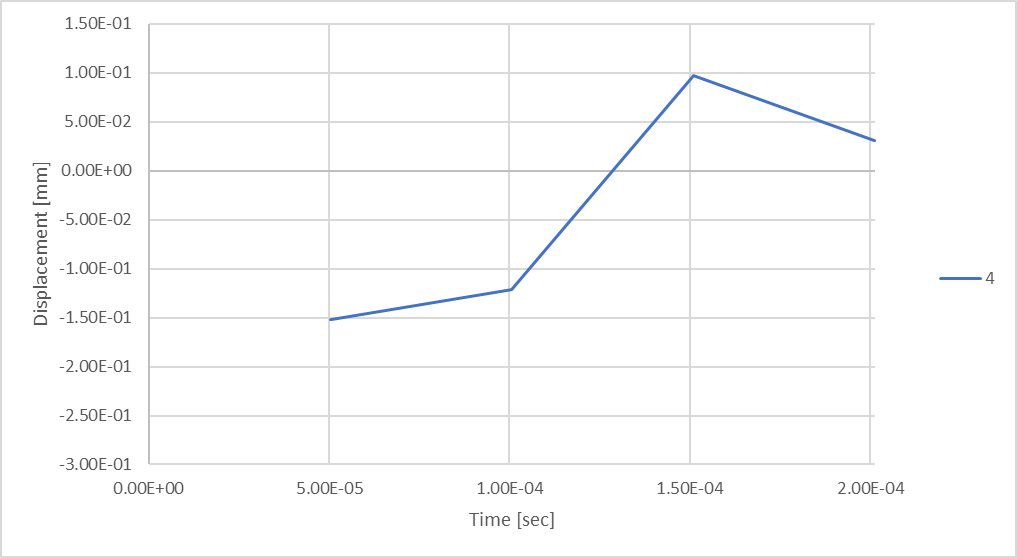
Figura 18: Deslocamento da haste ao considerar 4 etapas de tempo.
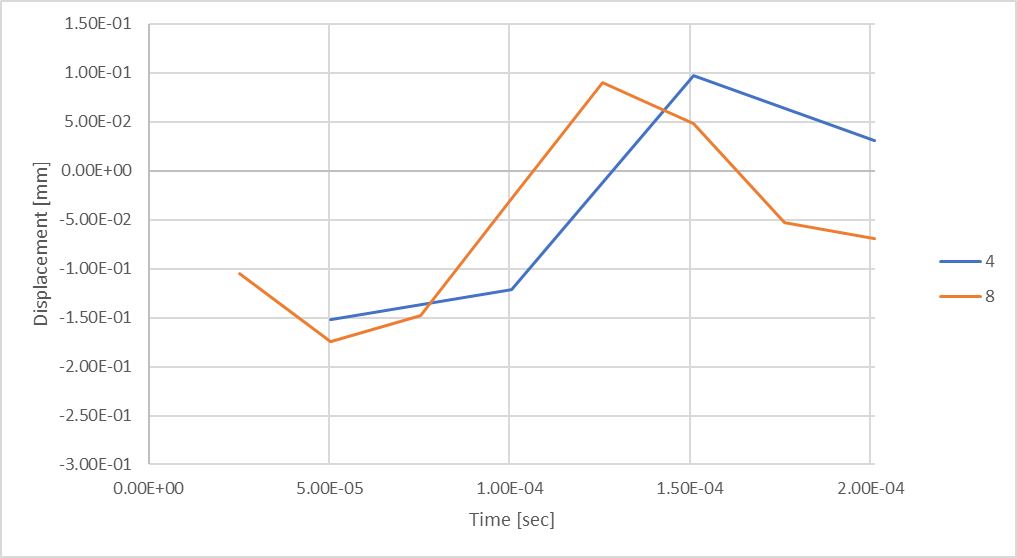
Figura 19: Deslocamento da haste considerando 8 passos de tempo.
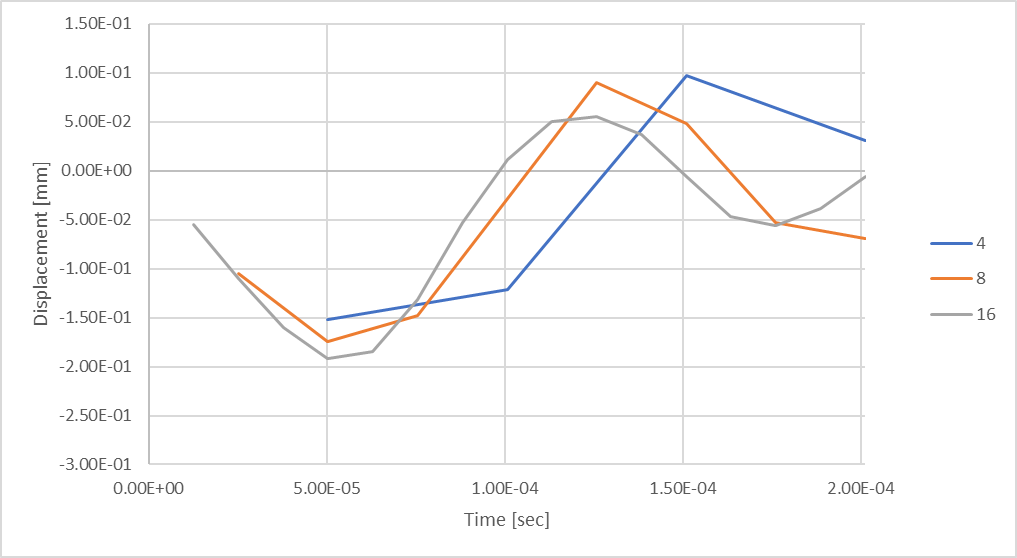
Figura 20: Com 16 passos de tempo, vemos deslocamentos de compressão da haste maiores.
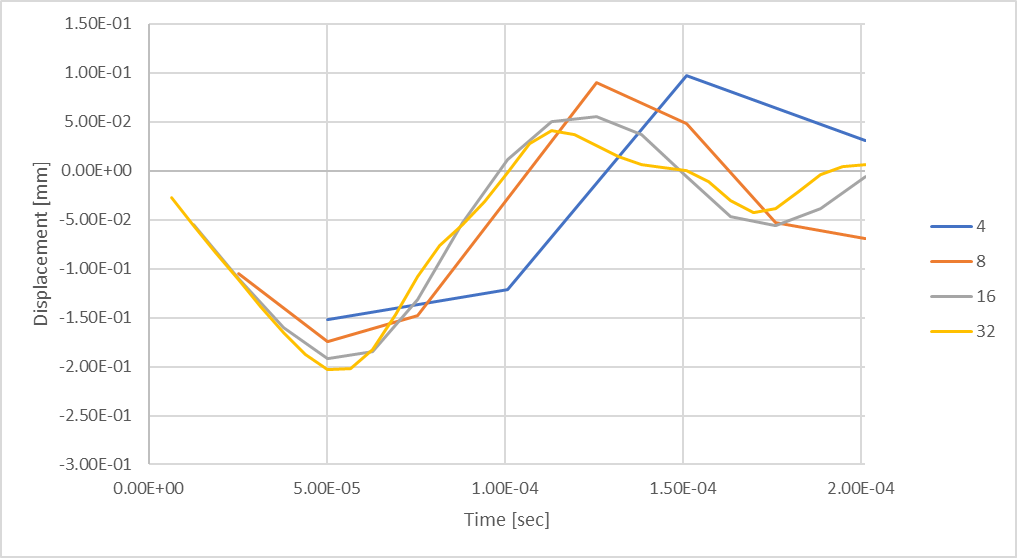
Figura 21: Deflexão máxima transitória da haste usando 32 passos de tempo.
Com base em nossa análise anterior do cálculo da magnitude senoidal média, descobrimos que, ao considerar 32 etapas, deveríamos esperar uma diferença de até 0,32% em relação aos resultados teóricos. No entanto, podemos ver que a resposta de deslocamento compressivo de nossa haste ainda está sendo formada em comparação com as explorações anteriores de etapas de tempo. O que acontece se considerarmos etapas de tempo adicionais?
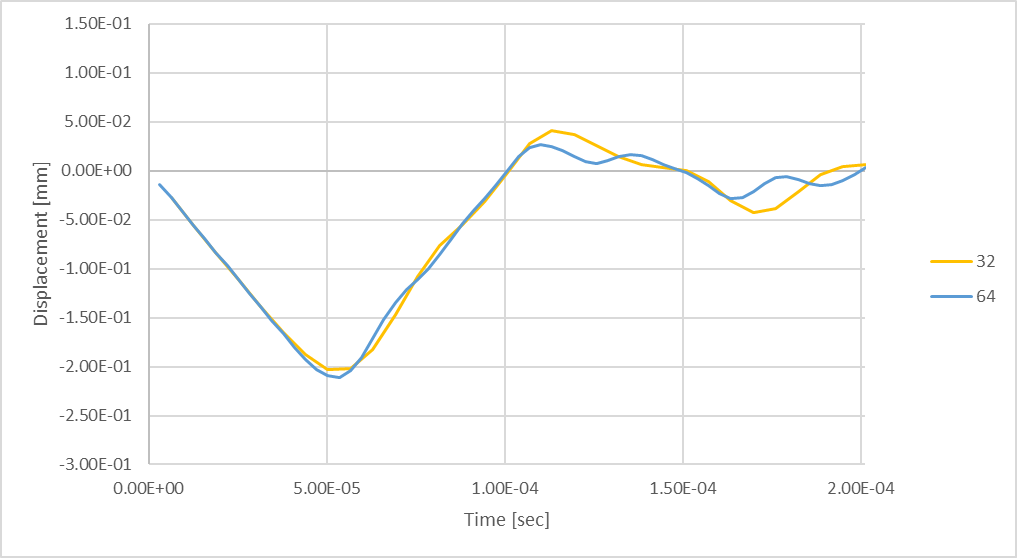
Figura 22: Deflexão máxima transitória da haste usando 64 etapas de tempo.
64 time-steps produz uma deflexão máxima da haste de compressão ligeiramente maior, mas em grande parte semelhante; no entanto, há sinais de oscilações de frequência mais alta sendo desenvolvidas durante o rebote da haste.
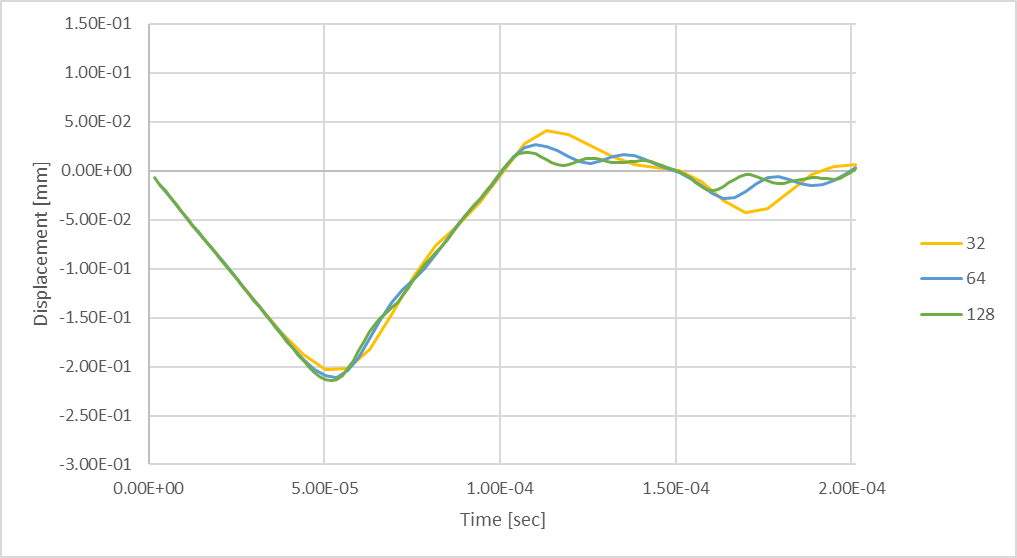
Figura 23: Deflexão máxima transitória da haste usando 128 passos de tempo.
Considerando 128 passos de tempo, o pico de compressão na haste é maior em relação ao menor número de passos de tempo. A deflexão compressiva máxima é 6% maior do que a produzida ao considerar 32 passos de tempo.
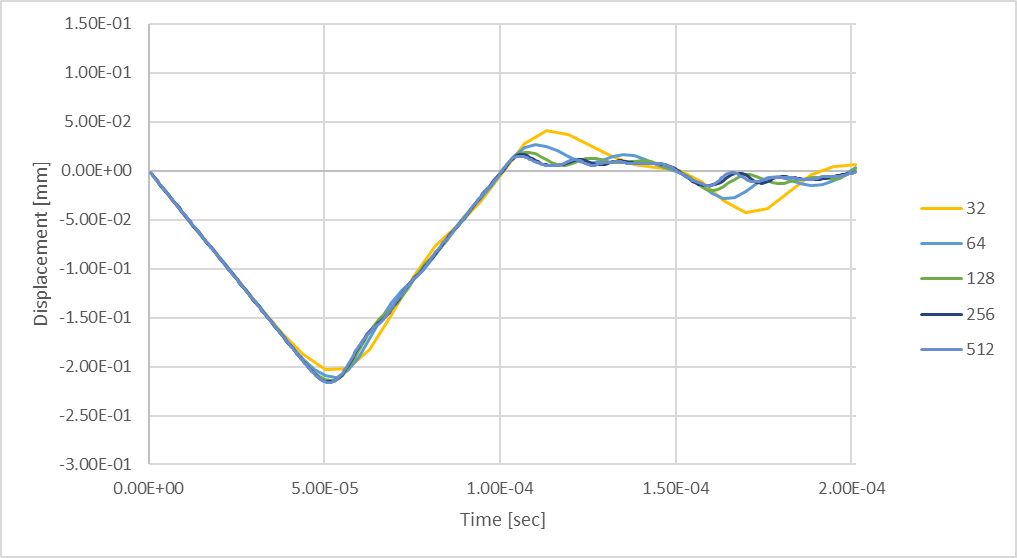
Figura 24: Deflexão máxima transitória da haste usando até 512 passos de tempo.
A comparação dos resultados da análise de 256 passos de tempo com os resultados produzidos pela consideração de 512 passos de tempo mostra que, ao considerar mais passos de tempo, é possível calcular uma resolução maior da resposta dinâmica. O gráfico a seguir ilustra como se pode esperar que as deflexões máximas da haste de compressão mudem em função do número de etapas de tempo consideradas em uma análise estrutural transitória.
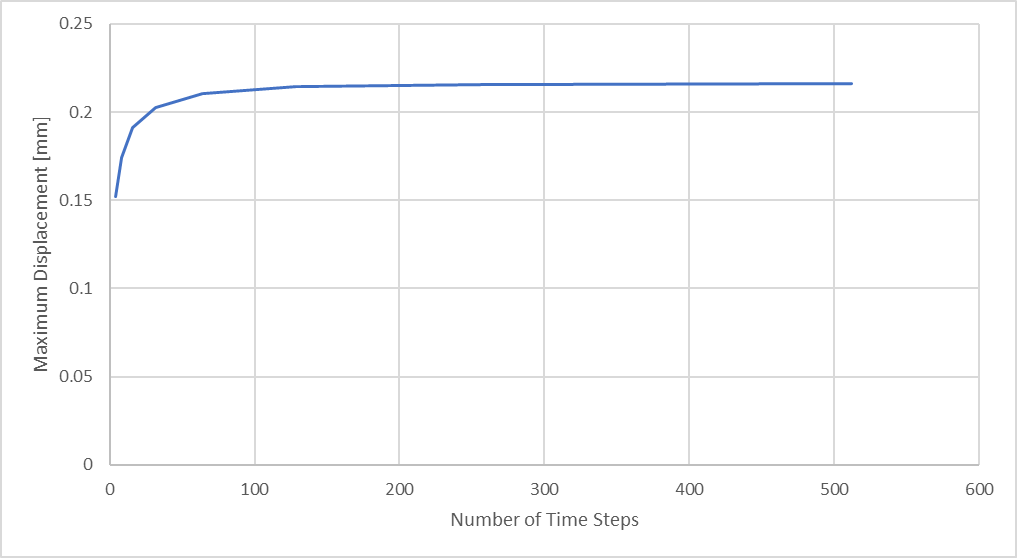
Figura 25: Deslocamento máximo de compressão da haste versus número de etapas de tempo de análise
Eventualmente, para um determinado tamanho de malha, chegamos a um ponto de retorno decrescente… em que o esforço envolvido com o tempo de análise prolongado e arquivos de resultados maiores não é justificado pela mudança significativa na magnitude dos resultados.
Com base nessas duas considerações, podemos ver que, ao usar 32 time-steps, podemos esperar caracterizar uma curva senoidal com até 0,32% de diferença, mas podemos produzir apenas resultados de deslocamento com 94% de precisão em comparação com a mesma análise que utilizou 512 time-steps, e apenas 91% de precisão em comparação com nossa deflexão máxima teórica. Na figura abaixo, vemos como nossos resultados de compressão máxima da haste se comparam ao máximo teoricamente estimado.
| Número de subetapas | Compressão máxima | Máxima teórica | Diferença de % |
| 4 | 0.152139 | 0.222859 | 31.73% |
| 8 | 0.174023 | 0.222859 | 21.91% |
| 16 | 0.191486 | 0.222859 | 14.08% |
| 32 | 0.202746 | 0.222859 | 9.03% |
| 64 | 0.210712 | 0.222859 | 5.45% |
| 128 | 0.214455 | 0.222859 | 3.77% |
| 256 | 0.215752 | 0.222859 | 3.19% |
| 512 | 0.216232 | 0.222859 | 2.97% |
Figura 26: Deslocamento máximo de compressão da haste versus etapas de tempo da análise
À medida que o número de etapas de tempo aumenta, a concordância entre nossos resultados de análise de elementos finitos e nosso valor derivado teoricamente aumenta.
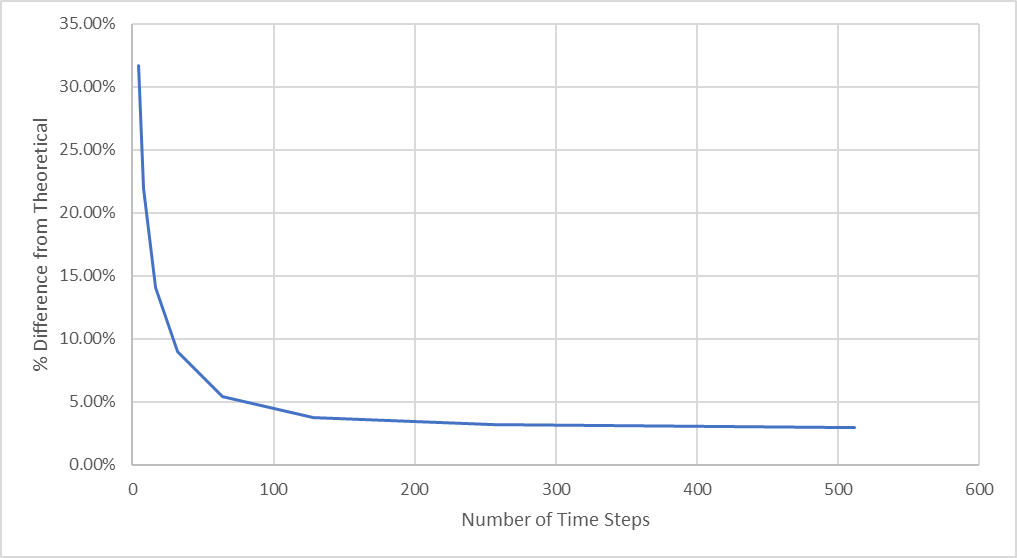
Figura 27: Diferença percentual em relação à deflexão máxima teórica
Vemos nessa figura como há uma melhora significativa em relação à convergência quando o número de etapas de tempo está entre 64 e 128, mas muda muito pouco quando o número de etapas de tempo aumenta.
Mas o que tudo isso significa em relação a outros resultados, como o estresse?
A seguir, plotarei a tensão máxima de von Mises por tempo para vários cenários de análise.
Figura 28: Tensão de von Mises durante a solução de 32 etapas de tempo
Figura 29: Tensão de von Mises durante a solução de 64 etapas de tempo
Figura 30: Tensão de von Mises durante a solução de 128 etapas de tempo
Figura 31: Tensão de von Mises durante a solução de 256 etapas de tempo
Figura 32: Tensão de von Mises durante a solução de 512 etapas de tempo
Em resumo, é isso que vemos ao visualizar as tensões:
| Número de subetapas | Tensão média máxima | Tensão máxima de pico | Diferença percentual da tensão média |
| 4 | 120.04 | 301.98 | 29.62% |
| 8 | 136.4 | 316.61 | 20.03% |
| 16 | 150.57 | 312.42 | 11.72% |
| 32 | 159.15 | 301.68 | 6.69% |
| 64 | 165.4 | 283.51 | 3.03% |
| 128 | 168.84 | 303.99 | 1.01% |
| 256 | 170.05 | 354.35 | 0.30% |
| 512 | 170.56 | 442.08 | 0.00% |
Figura 33: Deslocamento máximo de compressão da haste versus etapas de tempo da análise
Podemos ver que as tensões de impacto de pico tornam-se maiores à medida que o número de etapas de tempo aumenta, mostrando os maiores valores no início do impacto e tornando-se menores ao longo do evento. As tensões médias na haste vão de zero a um pico na compressão máxima e, em seguida, caem para zero após o término do impacto. Podemos plotar essas tensões médias máximas abaixo.
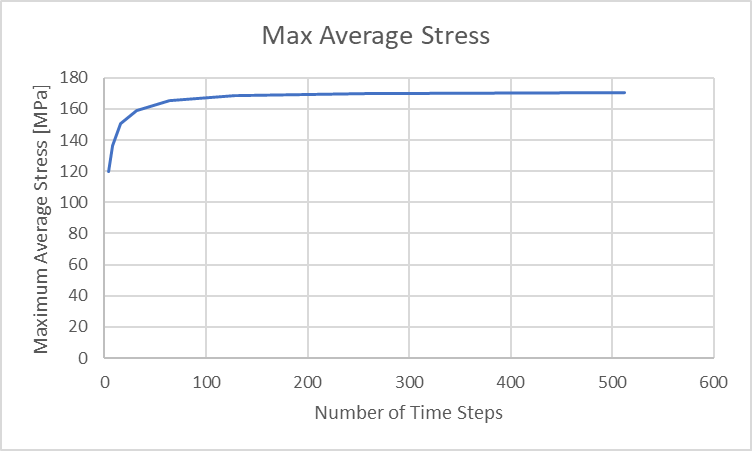
Figura 34: Deslocamento máximo de compressão da haste versus etapas de tempo da análise
Para colocar essas tensões médias máximas em perspectiva, podemos calcular uma tensão média máxima teórica em nossa haste da seguinte forma:
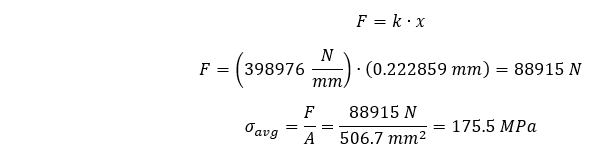
A plotagem de nossas tensões médias máximas novamente em comparação com a média máxima calculada teoricamente nos permite resumir a diferença percentual da seguinte forma:
| Número de subetapas | Tensão média máxima | Tensão média máxima teórica | Diferença de % |
| 4 | 120.04 | 175.5 | 31.60% |
| 8 | 136.4 | 175.5 | 22.28% |
| 16 | 150.57 | 175.5 | 14.21% |
| 32 | 159.15 | 175.5 | 9.32% |
| 64 | 165.4 | 175.5 | 5.75% |
| 128 | 168.84 | 175.5 | 3.79% |
| 256 | 170.05 | 175.5 | 3.11% |
| 512 | 170.56 | 175.5 | 2.81% |
Figura 35: Deslocamento máximo de compressão da haste versus etapas de tempo da análise
Mais uma vez, assim como ocorreu com as deflexões, reconhecemos uma melhoria significativa na diferença percentual de nossa tensão média máxima em comparação com a tensão média máxima calculada teoricamente ao considerar entre 64 e 128 etapas de tempo para o evento. No entanto, a utilização de mais etapas de tempo mostra pouca melhoria na precisão de nossos resultados.
Conclusão
Verificamos que os métodos de energia usados para estimar as deflexões máximas e as tensões médias para o evento dinâmico, como a queda de um objeto elástico em uma superfície rígida, podem produzir resultados razoáveis e que os aprimoramentos mais significativos na precisão ocorrem ao considerar entre 64 e 128 etapas de tempo para um evento igual ao período da frequência natural do nosso objeto impactante, calculado para a direção do impacto. Também descobrimos que o melhor método para aproximar essa frequência natural não é por meio de cálculos manuais, mas por meio de uma análise modal realizada usando o método de elementos finitos, especificamente porque a quantidade de massa efetiva modal participante pode não ser facilmente e
Participe do fórum para Designers!
Sua experiência é vital para a comunidade. Junte-se a nós e contribua com seu conhecimento!
Participe do fórum agoraCompartilhe, aprenda e cresça com os melhores profissionais do setor.

