Participe do fórum para Designers!
Sua experiência é vital para a comunidade. Junte-se a nós e contribua com seu conhecimento!
Participe do fórum agoraCompartilhe, aprenda e cresça com os melhores profissionais do setor.
O paradoxo dos dois capacitores é um experimento de pensamento provocativo criado para expor algumas das limitações da modelagem de circuitos elétricos, e muitas maneiras diferentes de resolver o paradoxo foram criadas. Acrescentarei uma solução à mistura que pode ser modelada no COMSOL Multiphysics® e depois expandi-lo para fazer e responder a uma pergunta ainda mais provocativa: A capacitância e a indutância existem? Vamos mergulhar de cabeça!
O Paradoxo dos Dois Capacitores
Esse experimento mental é geralmente apresentado da seguinte forma: Considere um dispositivo composto por dois capacitores equivalentes, com capacitância, C, conectados em paralelo com uma chave aberta entre eles. Todos os fios e capacitores são feitos de materiais ideais, perfeitamente livres de resistência e sem perdas. Um dos capacitores é carregado a um potencial, V_i, de modo que a carga armazenada é Q = CV_i. Não há diferença de potencial no outro capacitor, portanto, ele não tem carga armazenada. O que acontece quando o senhor fecha a chave?

Esquema do paradoxo de dois capacitores. Um capacitor tem uma diferença de potencial entre as placas. O que acontece quando a chave é fechada?
Algumas apresentações desse experimento de raciocínio lançam um arenque vermelho e afirmam que a carga no primeiro capacitor fluirá para o segundo, reduzindo a diferença de potencial no primeiro e aumentando-a no segundo até que um estado estável seja alcançado – momento em que a diferença de potencial é a mesma em ambos os capacitores e metade do V_ipois a carga é a mesma, Q, agora está distribuída em dois capacitores equivalentes. No entanto, isso leva imediatamente a um paradoxo, pois a energia em cada capacitor é W_C = \frac{1}{2} C \Delta V^2. Se a energia inicial for \frac{1}{2} C V_i^2 e a energia final é 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2, para onde foi a outra metade da energia?
Há muitas soluções disponíveis que invocam tudo, desde a mecânica quântica até a termodinâmica. É provável que todas essas soluções sejam válidas do ponto de vista educacional. Entretanto, muitas delas fazem um apelo implícito à realidade, dizendo que os fios e os capacitores simplesmente devem ter alguma resistência ou indutância. Mas por quê? Pelo menos no contexto de um experimento mental, pode ser razoável supor materiais perfeitamente sem perdas, negligenciando assim a resistência. Mas e quanto à indutância? No contexto desse experimento mental, podemos negligenciar a indutância? Vamos seguir essa pergunta e ver se ela oferece uma resposta interessante…
Uma solução simples para o paradoxo
Nosso dispositivo é composto por dois capacitores ideais e sem perdas. Mas mesmo um capacitor ideal deve separar espacialmente suas cargas. Ou seja, um capacitor deve ter algum tamanho. E se cada capacitor tem tamanho, então ele deve estar separado por alguma distância diferente de zero do outro capacitor. Portanto, se redesenharmos um pouco nosso diagrama, veremos que temos dois capacitores e dois meios loops de diâmetro finito de fio sem perdas, ao longo dos quais uma corrente variável no tempo pode fluir. Mas como chamamos essa estrutura? Indutor!
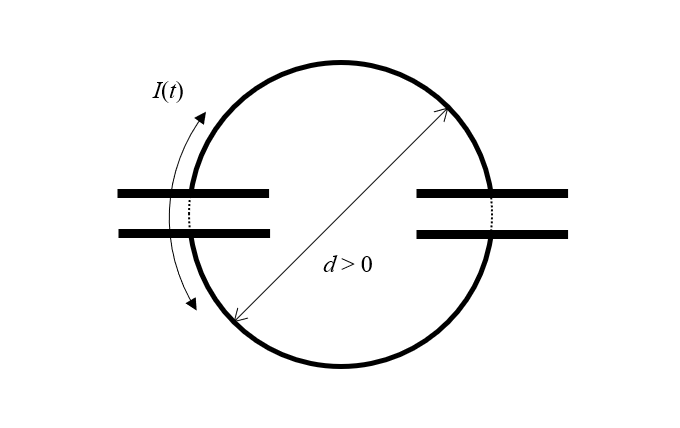
O paradoxo pode ser resolvido ao perceber que a estrutura deve ter um tamanho diferente de zero, com a corrente fluindo em torno de um loop de área finita e, portanto, também é um indutor.
A estrutura que desenhamos aqui deve ter tamanho finito e, portanto, também deve ter indutância, desde que exista em nosso universo, onde o espaço livre tem permeabilidade magnética. Portanto, simplesmente como consequência da existência de um capacitor em nosso circuito, também deve haver um indutor no circuito. Na verdade, isso fica ainda melhor: Se tivermos um indutor, mesmo sem perdas, qualquer corrente variável no tempo que flua através dele levará a um campo elétrico que existe entre as espiras do indutor e, portanto, qualquer indutor que adicionarmos a esse circuito também atuará como um capacitor! Poderíamos seguir essa linha lógica infinitamente, mas, para nossos propósitos, é suficiente apenas modificar nosso circuito com um único indutor que tenha indutância, L.
Agora temos um LC e isso tem uma solução analítica que esclarece imediatamente o paradoxo: a corrente fluirá para frente e para trás entre os capacitores e ao longo dos fios de comprimento finito, oscilando em uma frequência dada por: f=1/\sqrt{2\pi LC}. Nunca haverá uma solução de estado estável, portanto, nunca poderemos avaliar apenas a energia eletrostática. Também temos de considerar a energia devido às cargas em movimento, ou seja, o fluxo de corrente, I, e isso é dado por: W_L = \frac{1}{2} L I^2. A soma dessa energia elétrica e magnética (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) não se alterará com o tempo.
Verificação no COMSOL Multiphysics® Software
É fácil construir um modelo que verifique essa situação usando o COMSOL Multiphysics® e o módulo de RF. Faremos isso usando o Ondas eletromagnéticas, transientes juntamente com a interface do Eletrostática para calcular as condições iniciais. Modelaremos uma pequena região de vácuo perfeito com os capacitores e os fios em seu interior. As placas do capacitor, os fios e o espaço ao redor do nosso volume são todos tratados como condutores elétricos perfeitos, o que significa que os campos eletromagnéticos não penetrarão em nenhum limite. Há um guia para configurar esses modelos de descarga capacitiva em nosso artigo do Centro de Aprendizagem: “Modeling Capacitive Discharge” (Modelagem de descarga capacitiva).
A solução desse modelo no domínio do tempo e a avaliação da energia elétrica e magnética total mostram o comportamento oscilatório esperado. Também é possível dividir o domínio de modelagem em diferentes regiões para avaliar a energia total nas regiões ao redor dos dois capacitores, bem como no espaço circundante. Esse gráfico mostra como a energia oscila no espaço e no tempo.
Animação mostrando as correntes na superfície das placas e fios do capacitor, bem como o campo magnético no espaço entre eles.
As energias elétrica e magnética totais oscilam com o tempo; a soma não muda nesse dispositivo sem perdas.
O total da energia elétrica e magnética em diferentes domínios mostra que a energia oscila no tempo e no espaço.
Podemos observar que esses gráficos não são puramente senoidais no tempo, e devemos nos perguntar por que isso acontece. De onde vem esse conteúdo de frequência mais alta, ou seja, as ondulações na energia ao longo do tempo? Elas surgem da estrutura. É evidente que as duas placas têm uma capacitância bem definida, mas há também uma separação de carga devido aos fios, e toda essa estrutura fica dentro de uma cavidade cilíndrica que tem uma frequência de ressonância. Todas essas várias partes do dispositivo têm alguma contribuição para o comportamento eletromagnético. Cada contribuição pode ser bem pequena, mas sempre existe quando consideramos uma estrutura de tamanho finito.
Fazendo mais perguntas: A capacitância e a indutância existem?
Agora é hora de fazer uma pergunta mais provocativa sobre esse (ou qualquer outro) dispositivo eletromagnético: Ele tem capacitância ou indutância? Vimos claramente que esse dispositivo específico tem ambos. Mas e se o modificarmos adicionando um material dielétrico muito forte entre as placas do capacitor? Isso tornaria a capacitância muito maior, mas deixaria a indutância inalterada. E se tornássemos a capacitância muito maior, poderíamos dizer que a indutância não importa?
Em resumo: Não, nunca devemos pensar em um dispositivo eletrodinâmico como sendo puramente capacitivo ou puramente indutivo. Em um dispositivo eletrodinâmico, sempre haverá energia elétrica devido à separação espacial das cargas e energia magnética devido ao movimento das cargas. Embora às vezes possamos construir situações hipotéticas em que uma ou outra possa ser ignorada, devemos sempre lembrar que estamos fazendo uma simplificação mental.
Além disso, todos os materiais reais também têm alguma resistência finita, portanto, para sermos mais realistas, devemos falar de tudo como tendo uma impedância – e é nesse ponto que, às vezes, temos ainda mais problemas. Ao lidar com um modelo no domínio da frequência, existe uma expressão muito familiar para a impedância de um dispositivo elétrico:
Z = R + j\omega L -j\frac{1}{\omega C}
A resistência, R, nessa expressão, é uma medida de como a energia cinética das cargas em movimento, ou seja, a corrente, é convertida em energia térmica.
Essa equação é imediatamente reconhecível como relacionada a um oscilador harmônico amortecido de grau único de liberdade, que é um dos problemas mais bem estudados em engenharia e física. Sabemos que podemos calcular, a partir dessa expressão, a frequência ressonante e o fator de qualidade desse oscilador, e sabemos que os dispositivos reais têm uma ressonância fundamental e um fator de qualidade. Isso nos leva a equiparar os dois e tentar reduzir um dispositivo elétrico do mundo real, de tamanho finito, a uma única resistência, capacitância e indutância. Isso é um erro conceitual e nunca é válido porque a expressão acima para impedância só é aplicável a um dispositivo de tamanho infinitesimal.
Qualquer dispositivo real tem tamanho finito e, quando está operando em ressonância, a energia elétrica e magnética varia no espaço e no tempo, como vimos nos gráficos acima. Portanto, um modelo de circuito equivalente requer pelo menos três nós pelo menos três nós pelo menos três nós pelo menos três nós, embora, às vezes, muito mais. Voltando a pensar em nosso modelo físico dos dois capacitores e postulando que a placa de cada capacitor é representada por um nó no circuito elétrico, podemos ver que o modelo de circuito equivalente precisaria ser, no mínimo, tão complicado quanto o circuito ilustrado abaixo, com quatro nós. Observe que uma pequena capacitância foi adicionada em paralelo à indutância dos fios, pois também há uma separação de carga ao longo dos fios.
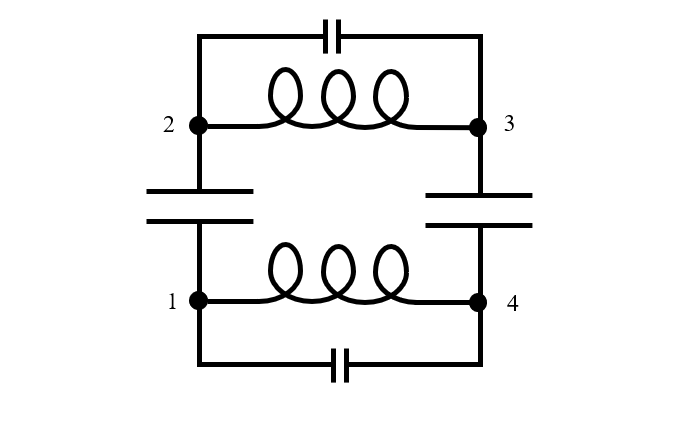
Um modelo de circuito equivalente de dois capacitores sem perdas de tamanho finito conectados em série.
Com esse exemplo, podemos ver que a construção de um modelo de circuito equivalente que seja válido próximo à ressonância pode se tornar rapidamente muito complexa, exigindo conhecimento físico, um pouco de experiência com dispositivos semelhantes e modelagem numérica.
Voltando à pergunta original, pode-se argumentar que a capacitância, a indutância e até mesmo a resistência são conceitos que não existem por si só – que existem apenas em combinação uns com os outros. Embora às vezes possamos reduzir a impedância dependente da frequência de um dispositivo a uma única resistência, capacitância e/ou indutância, essas simplificações só são válidas em frequências abaixo da ressonância do dispositivo. Ter isso em mente nos ajuda a evitar todos os tipos de armadilhas, desde esse divertido paradoxo de dois capacitores até problemas muito mais complexos e frustrantes do mundo real.
Comentários finais
Usamos aqui um experimento mental clássico para entender por que a impedância de um dispositivo eletromagnético operando próximo à ressonância não pode ser decomposta em uma única resistência, capacitância e indutância equivalentes. Experimentos mentais como o paradoxo dos dois capacitores são valiosos para ampliar nossa compreensão da eletromagnetismo e interpretar os resultados de nossos modelos computacionais.
Leitura adicional
O senhor está interessado em saber como a modelagem e a simulação podem ser usadas para resolver outros quebra-cabeças? Confira alguns outros exemplos no Blog da COMSOL:
Participe do fórum para Designers!
Sua experiência é vital para a comunidade. Junte-se a nós e contribua com seu conhecimento!
Participe do fórum agoraCompartilhe, aprenda e cresça com os melhores profissionais do setor.


