Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Все мы обращались к свойствам массы при работе с твердотельными моделями, особенно когда брали Сертификация SOLIDWORKS! По большей части полезная информация доступна с первого взгляда: Плотность, Масса, Объем, Площадь поверхности и т.д. Но как интерпретировать остальную информацию, содержащуюся в «Свойствах массы», особенно цифры внизу? О чем именно они нам говорят?
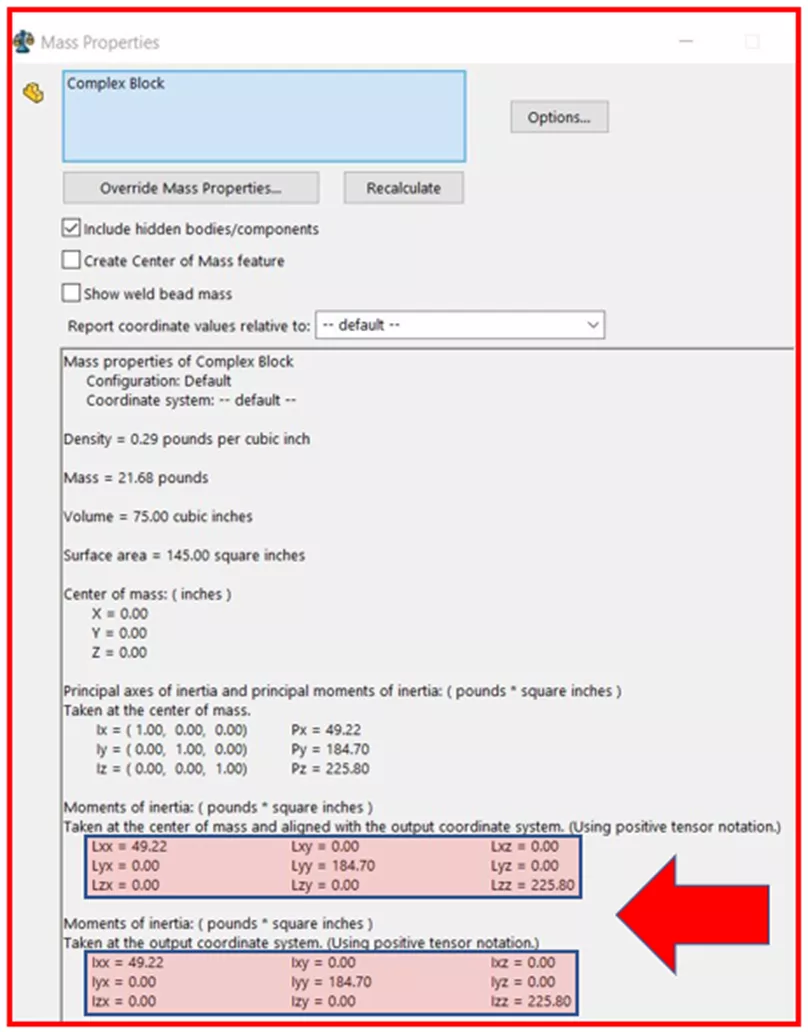
Все упирается в моменты инерции, которые зависят от массы, формы и оси объекта. вращения.
У каждого объекта есть центр масс, и если его подвесить в воздухе к этой точке, он будет идеально сбалансирован. Возьмем следующий симметричный сложный блок в качестве примера, мы можем видеть главные оси через его центр масс.
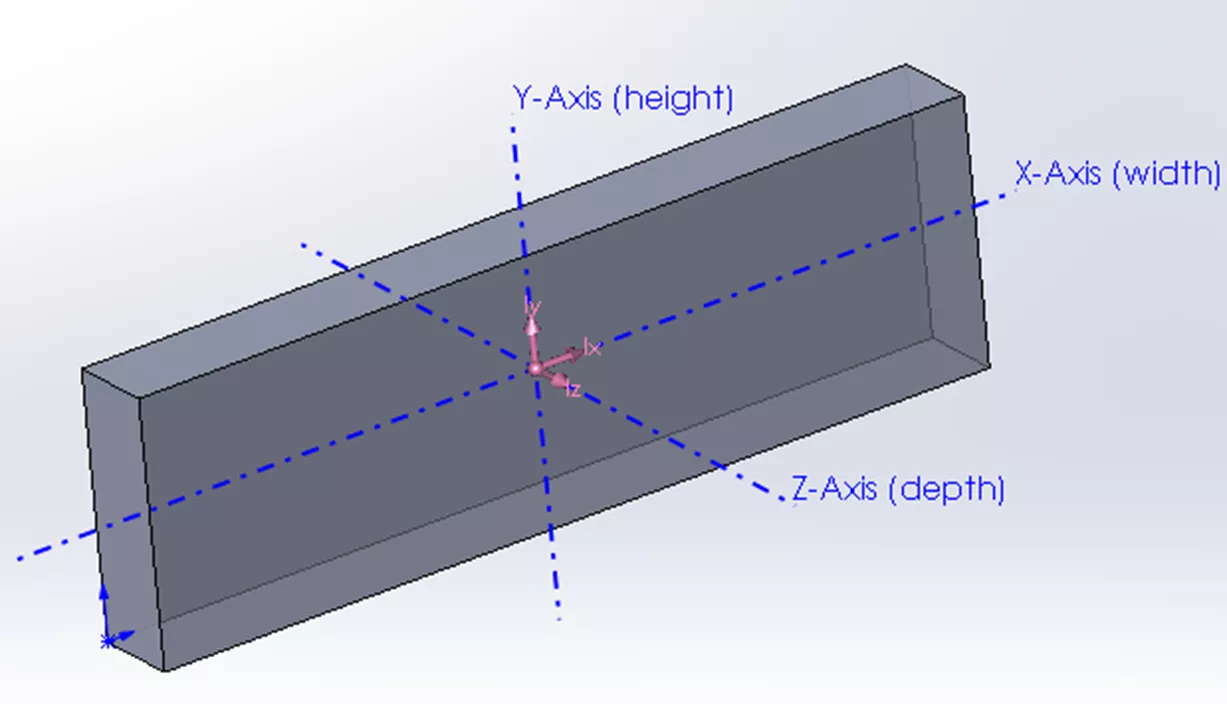
Если блок вращается вокруг любой из этих осей, мы увидим основные значения массы и момента инерции, которые отображаются в единицах ML2. Эти значения представляют собой распределение массы по каждой оси.

Группы чисел (матрицы 3×3) в нижней части окна «Свойства массы» представляют собой Тензоры инерции.

Если не вдаваться в технические подробности, то диагональные элементы этих матриц всегда представляют собой Моменты инерции масс относительно основных осей установленной системы координат. Любой недиагональный элемент представляет собой Перекрестный продукт MOI. Поперечное произведение MOI на самом деле просто указывает на симметрию объекта. Если он ненулевой, то можно ожидать внеосевого момента или ускорения, которые приведут к колебаниям объекта, а не к чистому вращению. Вспомните автомобильное колесо, которое сбалансировано для предотвращения шатания.
Рассмотрим пример объекта, который симметричен только относительно одной плоскости (XY):
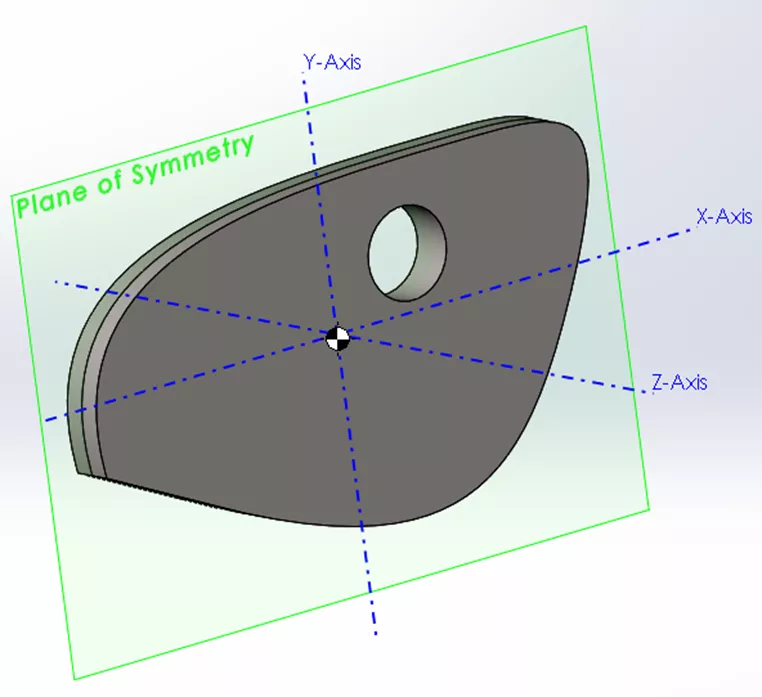
Здесь мы видим нулевые значения для всех поперечных произведений, содержащих ось Z (отсутствие колебаний в направлении Z). Это происходит потому, что масса объекта уравновешена одинаково вдоль этой оси по обе стороны от плоскости симметрии.

Один из способов интерпретации матричной нотации: если объект вращается вокруг оси X, то Lxx — это его инерция «против» вращения вокруг оси X, и одновременно Lxz — это его инерция «против» вращения вокруг оси Z.
Наконец, вы, вероятно, заметили, что свойства массы также дают значения MOI относительно Выходная система координат оси. OCS — это система координат по умолчанию при запуске детали, сборки и т. д., поэтому ее расположение зависит от того, как построена модель.
В следующем примере блок был создан экструзией вперед из начала координат по умолчанию (передняя плоскость), поэтому его OCS находится в нижнем заднем левом углу. Стоит отметить, что расположение выходной системы координат можно легко изменить даже после завершения работы над деталью. Эталонная геометрия.
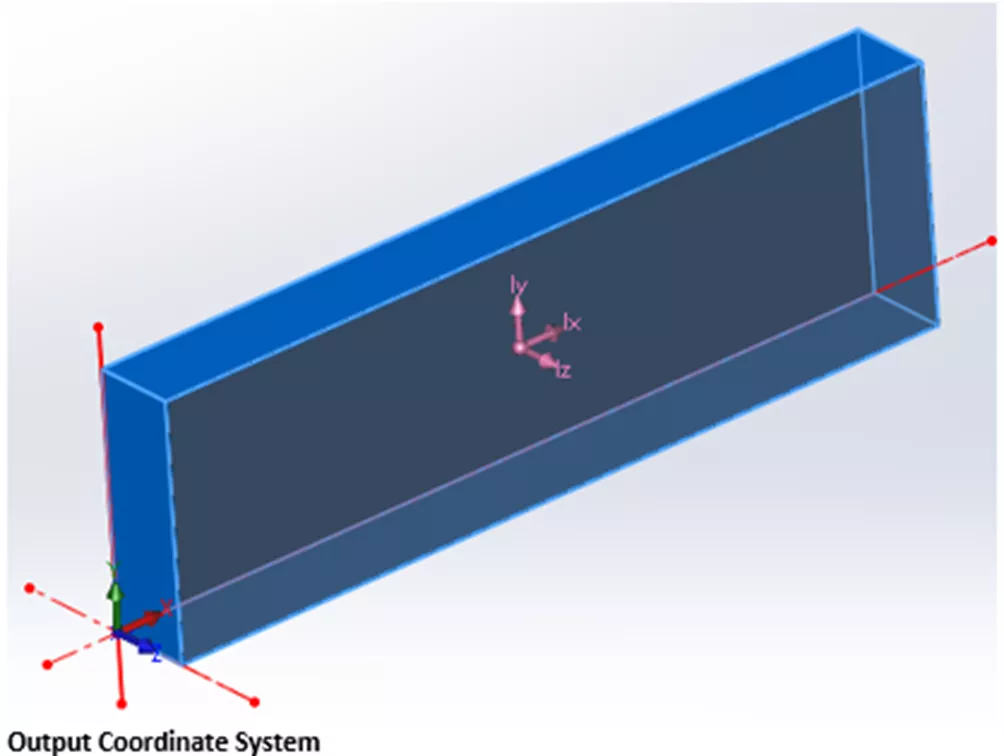
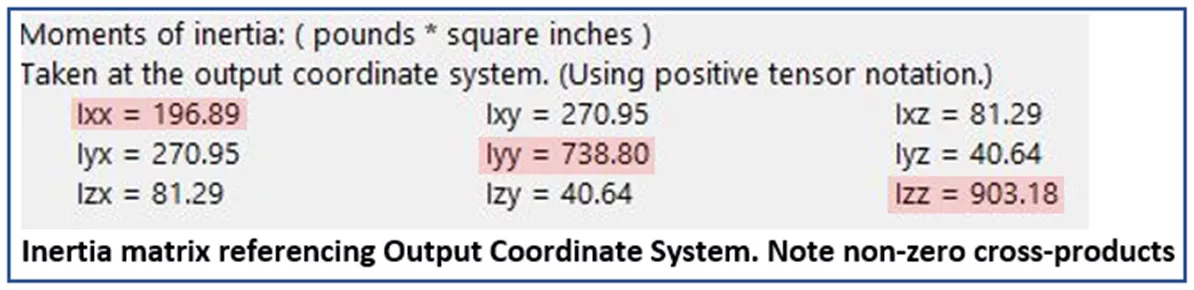
Нижняя матрица чисел в Mass-Properties вычисляется путем ссылки на Выходная система координат. В этом случае легко представить, что наша модель вращается вокруг осей OCS, и, как и следовало ожидать, моменты инерции намного больше. Снова мы видим МОИ относительно каждой оси, выраженные в диагональных элементах, но на этот раз, поскольку модель не симметрична относительно любой из осей OCS, мы видим ненулевые значения во всех кросс-продуктах.
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.

