Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Парадокс двух конденсаторов — это провокационный мысленный эксперимент, призванный выявить некоторые ограничения моделирования электрических цепей, и было разработано множество различных способов разрешения этого парадокса. Я добавлю в смесь решение, которое можно смоделировать в COMSOL Multiphysicals.® программное обеспечение, а затем расширить его, чтобы задать и ответить на еще более провокационный вопрос: существуют ли емкость и индуктивность? Давайте погрузимся!
Парадокс двух конденсаторов
Этот мысленный эксперимент обычно представляют следующим образом: Рассмотрим устройство, состоящее из двух эквивалентных конденсаторов емкостью С, подключенные параллельно с разомкнутым выключателем между ними. Все провода и конденсаторы изготовлены из идеальных материалов, не имеющих сопротивления и потерь. Один из конденсаторов заряжается до потенциала, В_ипоэтому накопленный заряд равен Q = CV_i. На другом конденсаторе нет разности потенциалов, поэтому он не имеет накопленного заряда. Что происходит, когда вы замыкаете переключатель?

Схема парадокса двух конденсаторов. Один конденсатор имеет разность потенциалов между обкладками. Что происходит, когда переключатель замыкается?
Некоторые презентации этого мысленного эксперимента будут отвлекать внимание и утверждать, что заряд первого конденсатора перетечет во второй, уменьшая разность потенциалов на первом и увеличивая его на втором до тех пор, пока не будет достигнуто устойчивое состояние — и в этот момент разность потенциалов одинакова на обоих конденсаторах и половине В_ипоскольку тот же заряд, вопрос, теперь распределяется по двум эквивалентным конденсаторам. Однако это немедленно приводит к парадоксу, поскольку энергия в каждом конденсаторе равна W_C = \frac{1}{2} C \Delta V^2. Если начальная энергия \frac{1}{2} C V_i^2 и конечная энергия 2 \frac{1}{2} C\left( V_i/2 \right)^2 «=» \frac{1}{4} C V_i^2куда делась вторая половина энергии?
Существует множество решений, которые задействуют все — от квантовой механики до термодинамики. Все эти решения, вероятно, действительны с образовательной точки зрения. Однако многие из них неявно апеллируют к реальности, утверждая, что провода и конденсаторы просто должны иметь некоторое сопротивление или некоторую индуктивность. Но почему? По крайней мере, в контексте мысленного эксперимента, возможно, было бы разумно предположить, что материалы абсолютно без потерь, пренебрегая таким образом сопротивлением. А как насчет индуктивности? Можем ли мы пренебречь индуктивностью в контексте этого мысленного эксперимента? Давайте проследим за этим вопросом и посмотрим, даст ли он интересный ответ…
Простое решение парадокса
Наше устройство состоит из двух идеальных конденсаторов без потерь. Но даже идеальный конденсатор должен пространственно разделять свои заряды. То есть конденсатор должен иметь какой-то размер. А если каждый конденсатор имеет размер, то он должен находиться на некотором ненулевом расстоянии от другого конденсатора. Итак, если мы немного перерисуем нашу схему, мы увидим, что у нас есть два конденсатора и две полупетли конечного диаметра из провода без потерь, по которым может течь изменяющийся во времени ток. Но как мы называем такую структуру? Индуктор!
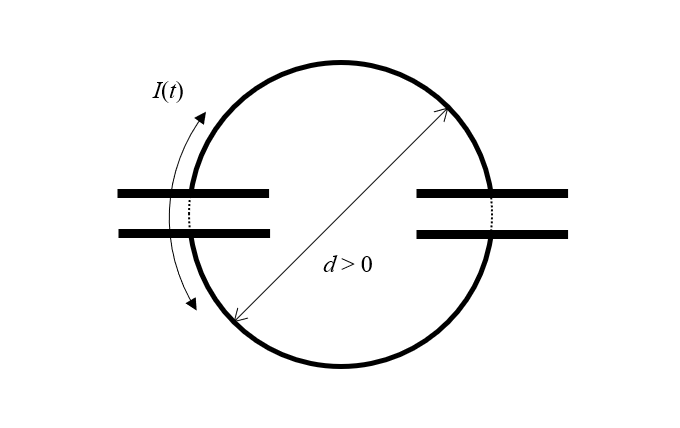
Парадокс можно разрешить, если осознать, что структура должна иметь ненулевой размер, при этом ток течет по петле конечной площади и, следовательно, также является индуктором.
Структура, которую мы здесь нарисовали, должна иметь конечный размер и, следовательно, она также должна обладать индуктивностью, пока она существует в нашей Вселенной, где свободное пространство обладает магнитной проницаемостью. Таким образом, просто потому, что в нашей цепи есть конденсатор, в цепи также должен быть и дроссель. На самом деле все становится даже лучше: если у нас есть индуктор, даже без потерь, любой изменяющийся во времени ток, протекающий через него, приведет к возникновению электрического поля, существующего между витками индуктора, и, следовательно, любого индуктора, который мы добавим к этому схема также действует как конденсатор! Мы могли бы следовать этой логике бесконечно, но для наших целей достаточно просто модифицировать нашу цепь с помощью одного индуктора, имеющего индуктивность л.
Теперь у нас есть ЛК Схема, и у нее есть аналитическое решение, которое сразу же проясняет парадокс: ток будет течь взад и вперед между конденсаторами и вдоль проводов конечной длины, колеблясь с частотой, определяемой формулой: f=1/\sqrt{2\pi LC}. Стационарного решения никогда не будет, поэтому мы никогда не сможем оценить только электростатическую энергию. Мы также должны учитывать энергию движущихся зарядов, т. е. поток тока, яи это определяется: W_L = \frac{1}{2} LI^2. Сумма этой электрической и магнитной энергии (\frac{1}{2} LI^2 + \frac{1}{2} CV^2) не изменится со временем.
Проверка в COMSOL Multiphysicals® Программное обеспечение
Построить модель, подтверждающую эту ситуацию, с помощью COMSOL Multiphysicals несложно.® и радиочастотный модуль. Мы сделаем это, используя Электромагнитные волны, переходные процессы интерфейс вместе с Электростатика интерфейс для расчета начальных условий. Мы смоделируем небольшую область идеального вакуума с конденсаторами и проводами внутри. Обкладки конденсатора, провода и пространство вокруг нашего объема считаются идеальными электрическими проводниками, а это означает, что электромагнитные поля не проникнут через какие-либо границы. Руководство по настройке таких моделей емкостного разряда можно найти в статье нашего Центра обучения: «Моделирование емкостного разряда».
Решение этой модели во временной области и оценка общей электрической и магнитной энергии показывает ожидаемое колебательное поведение. Также возможно разделить область моделирования на разные области, чтобы оценить полную энергию в областях вокруг двух конденсаторов, а также в окружающем пространстве. Этот график показывает, как энергия колеблется как в пространстве, так и во времени.
Анимация, показывающая токи на поверхности пластин и проводов конденсатора, а также магнитное поле в пространстве между ними.
Общая электрическая и магнитная энергия колеблется со временем; сумма не меняется в этом устройстве без потерь.
Сумма электрической и магнитной энергии в разных областях показывает, что энергия колеблется во времени и пространстве.
Мы можем заметить, что эти графики не являются чисто синусоидальными во времени, и нам следует задаться вопросом, почему это так. Откуда берется это высокочастотное содержание, то есть пульсации энергии во времени? Они возникают из структуры. Совершенно очевидно, что две пластины имеют четко определенную емкость, но существует также разделение зарядов из-за проводов, и вся эта конструкция находится внутри цилиндрической полости, имеющей резонансную частоту. Все эти различные части устройства вносят определенный вклад в электромагнитное поведение. Каждый вклад может быть весьма небольшим, но он всегда существует, когда мы рассматриваем структуру конечного размера.
Задавайте больше вопросов: существуют ли емкость и индуктивность?
Теперь пришло время задать более провокационный вопрос об этом (или любом другом) электромагнитном устройстве: есть ли у него емкость или индуктивность? Мы ясно видели, что это конкретное устройство имеет и то, и другое. Но что, если мы модифицируем его, добавив очень прочный диэлектрический материал между пластинами конденсатора? Это сделает емкость намного больше, но индуктивность останется неизменной. А если бы мы сделали емкость намного больше, могли бы мы сказать, что индуктивность не имеет значения?
Короче говоря: нет, мы никогда не должны думать об электродинамическом устройстве как о чисто емкостном или чисто индуктивном устройстве. В электродинамическом устройстве всегда будет электрическая энергия за счет пространственного разделения зарядов и магнитная энергия за счет движения зарядов. Хотя иногда мы можем создавать гипотетические ситуации, в которых одно или другое можно игнорировать, мы всегда должны помнить, что мы делаем мысленное упрощение.
Более того, все реальные материалы также обладают некоторым конечным сопротивлением, поэтому, чтобы быть более реалистичными, мы должны говорить обо всем как о наличии импеданса — и здесь мы иногда попадаем в еще большие проблемы. Когда речь идет о модели в частотной области, существует очень знакомое выражение для импеданса электрического устройства:
Z = R + j\omega L -j\frac{1}{\omega C}
Сопротивление, рв этом выражении является мерой того, как кинетическая энергия движущихся зарядов, т. е. ток, преобразуется в тепловую энергию.
В этом уравнении сразу можно узнать, что оно относится к затухающему гармоническому генератору с одной степенью свободы, что является одной из наиболее хорошо изученных проблем в технике и физике. Мы знаем, что из этого выражения можно вычислить резонансную частоту и добротность такого генератора, и мы знаем, что реальные устройства имеют фундаментальный резонанс и добротность. Это побуждает нас приравнять их и попытаться свести реальное электрическое устройство конечного размера к одному сопротивлению, емкости и индуктивности. Это концептуальная ошибка, и она никогда не бывает верной, поскольку приведенное выше выражение для импеданса применимо только к устройству бесконечно малого размера.
Любое реальное устройство имеет конечный размер, и когда оно работает в резонансе, электрическая и магнитная энергия изменяются в пространстве и времени, как мы видели на графиках выше. Следовательно, модель эквивалентной схемы требует как минимум трех узлов, хотя иногда и намного больше. Возвращаясь к нашей физической модели двух конденсаторов и постулируя, что обкладка каждого конденсатора представлена узлом в электрической цепи, мы видим, что модель эквивалентной схемы должна быть по крайней мере такой же сложной, как схема, изображенная на рисунке. ниже, с четырьмя узлами. Обратите внимание, что параллельно индуктивности проводов добавлена небольшая емкость, поскольку вдоль проводов также происходит разделение заряда.
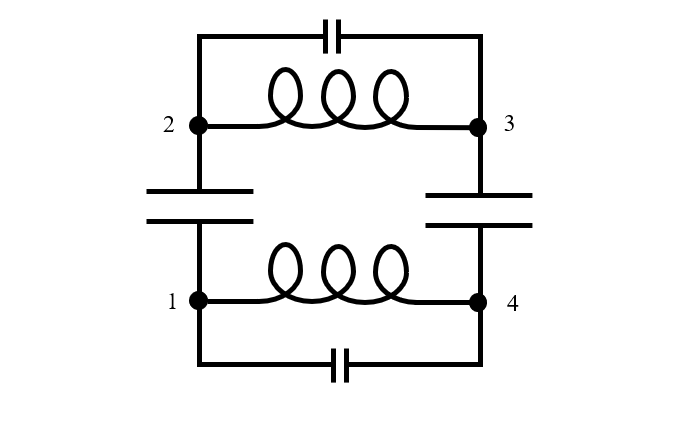
Модель эквивалентной схемы двух конденсаторов без потерь конечного размера, соединенных последовательно.
Мы надеемся, что из этого примера мы увидим, что построение модели эквивалентной схемы, пригодной для вблизи резонанса, может быстро стать очень сложной задачей, требующей физического понимания, большого опыта работы с аналогичными устройствами и численного моделирования.
Возвращаясь к исходному вопросу, можно утверждать, что емкость, индуктивность и даже сопротивление — это понятия, которые не существуют сами по себе — они существуют только в сочетании друг с другом. Хотя иногда мы можем уменьшить частотно-зависимое сопротивление устройства до одного сопротивления, емкости и/или индуктивности, такие упрощения действительны только на частотах ниже резонанса устройства. Помня об этом, мы можем избежать всевозможных ловушек, начиная от занимательного парадокса двух конденсаторов и заканчивая гораздо более удручающе сложными проблемами реального мира.
Заключительные замечания
Мы использовали здесь классический мысленный эксперимент, чтобы понять, почему полное сопротивление электромагнитного устройства, работающего вблизи резонанса, не может быть разложено на одно эквивалентное сопротивление, емкость и индуктивность. Мысленные эксперименты, такие как парадокс двух конденсаторов, ценны для расширения нашего понимания электромагнетизма и интерпретации результатов наших вычислительных моделей.
Дальнейшее чтение
Хотите узнать, как моделирование и моделирование можно использовать для решения других головоломок? Ознакомьтесь с другими примерами в блоге COMSOL:
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.


