Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Методы, доступные в качестве драйверов адаптеров в Process Composer, великолепны. Они являются результатом глубоких исследований численных методов. Наиболее известными методами являются DOE, оптимизация, аппроксимации, шесть сигм. Мы подробно обсуждали DOE в предыдущих блогах. В этом блоге мы углубимся в оптимизацию. Давайте не будем забывать, что мы находимся в процессе компоновки, поэтому оптимизация параметрическая, в первую очередь обусловленная геометрическими или физическими параметрами.
Классическое определение оптимизации
У вас есть мяч где-то на огороженном поле. У вас есть отправная точка. Вам нужно найти мяч, пройдя минимальное расстояние, не пересекая забор. У вас есть датчики для помощи. Мяч – это целевая функция. Заборы – это ограничения. Датчики — это используемые методы оптимизации.

Разница между планированием экспериментов и оптимизацией
Разница между ними такая же, как разница между «лучшим» и «лучшим». Планирование экспериментов — это метод эффективного выбора наиболее подходящей проектной точки из пула существующего набора точек. Этот набор может быть определен либо пользователем, либо самим УОО. Методы оптимизации начинаются с одной начальной точки проектирования и итеративно перемещаются в пространстве проектирования, чтобы добраться до оптимальной или лучшей точки проектирования. В зависимости от проблемы DOE может стать предшественником оптимизации.
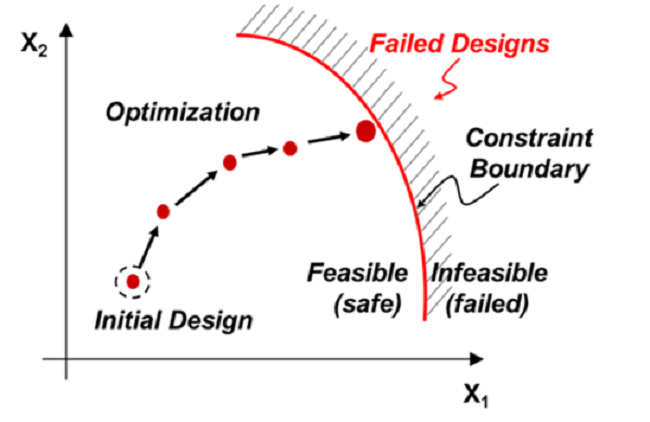
Типы методов оптимизации
Существуют разные методы их классификации в зависимости от того, как определена целевая функция, и типа подходящего проектного пространства.
Ограниченные методы: Для работы они используют отдельные функции: одну для целей, другую для ограничений. Все мы на каком-то уровне видели подобные методы на инженерных курсах. Они являются наиболее распространенными.
Минимизировать/максимизировать F(x) в x1>x>x2
При условии: h(x)>a1; г(х)>а2; f(x)=0 и т. д.
Неограниченные методы: Они используют только одну функцию как для целей, так и для ограничений. Пользователь по-прежнему определяет ограничения отдельно от цели, но внутренне ограниченная проблема преобразуется в неограниченную задачу.
В зависимости от применения к различным типам проектного пространства методы оптимизации можно разделить на градиентные, прямые или исследовательские. Сокращения, показанные на изображениях ниже, представляют собой названия методов в соответствующих категориях.
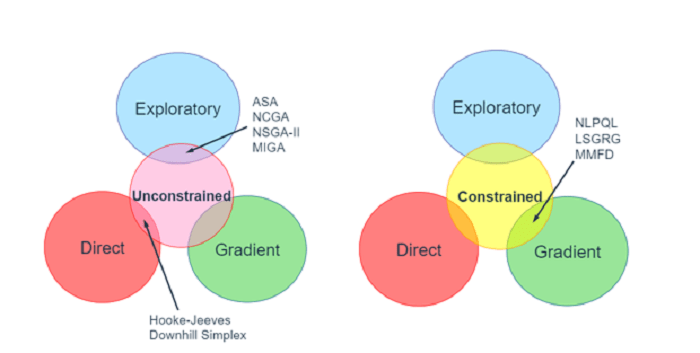
Градиентные методы: Они являются самыми старыми и хорошо протестированы в отрасли. Они работают по принципу минимальной энергии или максимальной стабильности. Вы осторожно бросаете мяч в долину, и он будет скользить по пути наибольшего падения, пока не достигнет самой низкой точки в окрестностях. Эти методы работают в непрерывном пространстве проектирования, которое имеет непрерывность C0 и C1. Они, скорее всего, застрянут в локальных минимумах, поэтому начальную точку следует выбирать осторожно.

Прямые методы: Алгоритм прямого поиска начинается с базовой точки. Он ищет множество точек вокруг себя в поисках той, в которой значение целевой функции ниже текущего. Алгоритм переходит к этой точке как к новой базовой точке и ищет новый набор точек вокруг нее. Можно понять, что такой метод эффективен в вычислительном отношении, поскольку не требуется расчет градиента. Он более универсален, поскольку не требуется непрерывность C0 и C1. Наиболее распространенными из них являются Гук-Дживс и Даунхилл Симплекс.
Метод Гука-Дживса отслеживает направление движения. Он не меняет свое направление при каждом шаге, если по ходу движения имеется нижняя точка.

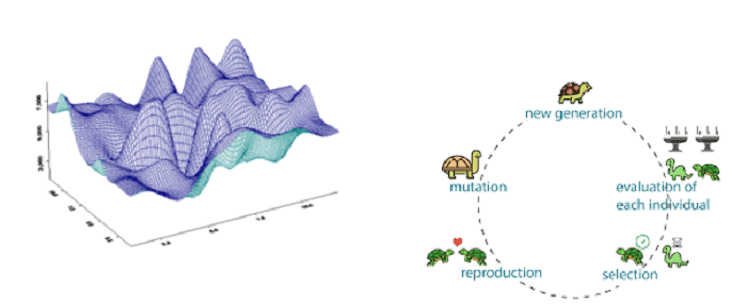
Исследовательские методы: Эти методы основаны на методах пересечения или мутации одного набора данных точек, называемых родительскими, для создания другого набора данных точек, называемых дочерними. Новый набор данных развивается с каждой мутацией и приближается к оптимальному решению. Это схема высокой точности, которая работает со всеми видами целевых функций: разрывными, недифференцируемыми, стохастическими, смешанного целочисленного типа и сильно нелинейными с множеством пиков и впадин, как показано ниже. Однако это самая дорогая схема оптимизации с точки зрения вычислительных затрат. Наиболее распространенными методами являются генетический алгоритм, рой частиц и адаптивный моделируемый отжиг.
Методы на основе указателей: это смешанный подход на случай, если пользователь не знает, какой тип метода будет наиболее подходящим для решения проблемы с достаточной точностью. Указательный подход может помочь, когда пользователь сталкивается с незнакомым типом проектного пространства, которое трудно визуализировать. Метод указателя может использовать до трех схем оптимизации, желательно по одной из каждой корзины: градиентную, прямую и исследовательскую. По мере оптимизации алгоритм отслеживает эффективность каждого метода и использует тот, который наиболее подходит для данной задачи.
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.

