İki Kapasitör Paradoksundan Öğrenmek: Kapasitans ve Endüktans Var mı?

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.

İki kapasitör paradoksu, elektrik devresi modellemenin bazı sınırlamalarını ortaya çıkarmak için kurulmuş provokatif bir düşünce deneyidir ve paradoksu çözmenin birçok farklı yolu tasarlanmıştır. Karışıma COMSOL Multiphysics'te modellenebilecek bir çözüm ekleyeceğim^® yazılımını genişletin ve daha da kışkırtıcı bir soruyu sorup yanıtlayın: Kapasitans ve endüktans var mı? Hadi dalalım!

İki Kapasitör Paradoksu

Bu düşünce deneyi genellikle şu şekilde sunulur: İki eşdeğer kapasitörden oluşan, kapasitanslı bir cihaz düşünün, C, aralarında açık bir anahtarla paralel olarak bağlanır. Tüm kablolar ve kapasitörler ideal, mükemmel dirençsiz, kayıpsız malzemelerden yapılmıştır. Kapasitörlerden biri potansiyele göre şarj edilir, V_iyani depolanan yük S = CV_i. Diğer kapasitörde potansiyel fark olmadığından depolanmış yükü yoktur. Anahtarı kapattığınızda ne olur?

İki kapasitör paradoksunun şeması. Bir kondansatörün plakaları arasında potansiyel farkı vardır. Anahtar kapatıldığında ne olur?

Bu düşünce deneyinin bazı sunumları yanıltıcı olacak ve ilk kapasitördeki yükün ikinciye akacağını, birincideki potansiyel farkı azaltacağını ve ikincideki potansiyel farkı kararlı bir duruma ulaşılıncaya kadar artıracağını iddia edecek – bu noktada potansiyel fark hem kapasitörlerde hem de yarısında aynıdır V_iaynı ücret olduğundan, Q, artık iki eşdeğer kapasitöre yayılmıştır. Ancak bu hemen bir paradoksa yol açar, çünkü her kapasitördeki enerji W_C = \frac{1}{2} C \Delta V^2. Başlangıç ​​enerjisi ise \frac{1}{2} C V_i^2 ve son enerji 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2Enerjinin diğer yarısı nereye gitti?

Kuantum mekaniğinden termodinamiğe kadar her şeyi içeren birçok çözüm mevcut. Bu çözümlerin tümü muhtemelen eğitim açısından geçerlidir. Ancak birçoğu, kabloların ve kapasitörlerin bir miktar dirence veya bir miktar endüktansa sahip olması gerektiğini söyleyerek gerçeğe örtülü bir çağrıda bulunuyor. Ama neden? En azından bir düşünce deneyi bağlamında, malzemelerin tamamen kayıpsız olduğunu varsaymak, dolayısıyla direnci ihmal etmek mantıklı olabilir. Peki ya endüktans? Bu düşünce deneyi bağlamında endüktansı ihmal edebilir miyiz? Gelin bu soruyu takip edelim ve ilginç bir cevap verip vermeyeceğini görelim…

Paradoksa Basit Bir Çözüm

Cihazımız iki adet ideal, kayıpsız kapasitörden oluşmaktadır. Ancak ideal bir kondansatörün bile yüklerini mekansal olarak ayırması gerekir. Yani bir kapasitörün belirli bir boyuta sahip olması gerekir. Ve eğer her kapasitörün boyutu varsa, o zaman diğer kapasitörden sıfırdan farklı bir mesafe ile ayrılmalıdır. Diyagramımızı biraz yeniden çizersek, iki kapasitörümüz ve üzerinde zamanla değişen bir akımın akabileceği iki adet sonlu çaplı, kayıpsız telin olduğunu görürüz. Peki böyle bir yapıya ne diyoruz? Bir indüktör!

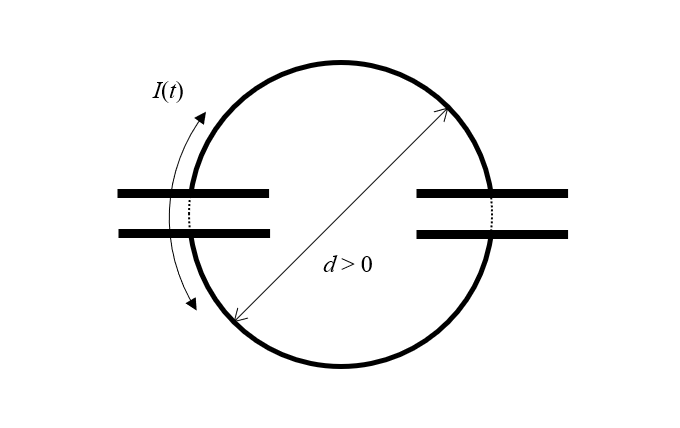
Paradoks, yapının sıfırdan farklı bir boyuta sahip olması gerektiği, akımın sonlu alanlı bir döngü etrafında aktığı ve dolayısıyla aynı zamanda bir indüktör olduğu fark edilerek çözülebilir.

Burada çizdiğimiz yapının, boş uzayın manyetik geçirgenliğe sahip olduğu evrenimizde var olduğu sürece, sonlu büyüklükte olması ve dolayısıyla endüktansa da sahip olması gerekir. Yani devremizde bir kapasitör bulunmasının bir sonucu olarak devrede bir indüktörün de bulunması gerekir. Aslında daha da iyi oluyor: Eğer bir indüktörümüz varsa, kayıpsız olsa bile, içinden geçen zamanla değişen herhangi bir akım, indüktörün dönüşleri arasında var olan bir elektrik alanına ve dolayısıyla buna eklediğimiz herhangi bir indüktöre yol açacaktır. devre aynı zamanda kapasitör görevi de görür! Bu mantık dizisini sonsuza kadar takip edebiliriz, ancak amaçlarımız açısından devremizi yalnızca endüktansı olan tek bir indüktörle değiştirmek yeterlidir, L.

Artık elimizde bir LC Bu, paradoksu anında ortadan kaldıran analitik bir çözüme sahiptir: Akım, kapasitörler arasında ve sonlu uzunluktaki teller boyunca ileri geri akacak ve aşağıdaki şekilde verilen bir frekansta salınacaktır: f=1/\sqrt{2\pi LC}. Hiçbir zaman kararlı durum çözümü olmayacağından elektrostatik enerjiyi hiçbir zaman tek başına değerlendiremeyiz. Ayrıca hareketli yüklerden, yani akımın akışından kaynaklanan enerjiyi de dikkate almalıyız. BENve bu şu şekilde verilir: W_L = \frac{1}{2} LI^2. Bu elektrik ve manyetik enerjinin toplamı (\frac{1}{2} LI^2 + \frac{1}{2} CV^2) zamanla değişmeyecektir.

COMSOL Multiphysics'te doğrulama^® Yazılım

COMSOL Multiphysics kullanarak bu durumu doğrulayan bir model oluşturmak çok kolaydır.^® ve RF Modülü. Bunu kullanarak yapacağız Elektromanyetik Dalgalar, Geçici arayüzü ile birlikte Elektrostatik Başlangıç ​​koşullarını hesaplamak için arayüz. İçerisindeki kapasitörler ve kablolarla küçük bir mükemmel vakum bölgesini modelleyeceğiz. Hacimimizin etrafındaki kapasitör plakaları, kablolar ve boşluk, mükemmel elektrik iletkenleri olarak kabul edilir; bu, elektromanyetik alanların hiçbir sınırdan geçmeyeceği anlamına gelir. Bu tür kapasitif deşarj modellerini kurmaya yönelik Öğrenim Merkezi makalemizde bir kılavuz bulunmaktadır: “Kapasitif Deşarjın Modellenmesi”.

Bu zaman alanı modelinin çözülmesi ve toplam elektrik ve manyetik enerjinin değerlendirilmesi, beklenen salınım davranışını gösterir. İki kapasitörün etrafındaki bölgelerdeki ve çevredeki alandaki toplam enerjiyi değerlendirmek için modelleme alanını farklı bölgelere bölmek de mümkündür. Bu çizim enerjinin hem uzayda hem de zamanda nasıl salındığını gösterir.

Kapasitör plakaları ve tellerinin yüzeyindeki akımları ve aradaki boşluktaki manyetik alanı gösteren animasyon.

Toplam elektrik ve manyetik enerji zamanla salınır; bu kayıpsız cihazda toplam değişmez.

Farklı alanlardaki elektrik ve manyetik enerjinin toplamı, enerjinin zaman ve uzayda salındığını gösterir.

Bu grafiklerin zaman açısından tamamen sinüzoidal olmadığını gözlemleyebiliriz ve bunun nedenini sormalıyız. Bu yüksek frekanslı içerik, yani enerjinin zaman içindeki dalgalanmaları nereden geliyor? Yapıdan kaynaklanırlar. İki plakanın iyi tanımlanmış bir kapasitansa sahip olduğu oldukça açıktır, ancak aynı zamanda kablolardan dolayı bir yük ayrımı da vardır ve tüm bu yapı, rezonans frekansına sahip silindirik bir boşluk içinde yer alır. Cihazın tüm bu çeşitli parçalarının elektromanyetik davranışa bir miktar katkısı vardır. Her bir katkı oldukça küçük olabilir ancak sonlu boyutlu bir yapıyı düşündüğümüzde her zaman mevcuttur.

Daha Fazla Soru Sormak: Kapasitans ve Endüktans Var mı?

Artık bu (veya başka herhangi bir) elektromanyetik cihaz hakkında daha kışkırtıcı bir soru sormanın zamanı geldi: Bir kapasitansı veya endüktansı var mı? Bu özel cihazın her ikisine de sahip olduğunu açıkça gördük. Peki ya kapasitör plakaları arasına çok güçlü bir dielektrik malzeme ekleyerek onu değiştirseydik? Bu, kapasitansı çok daha büyük hale getirir ancak endüktansı değiştirmeden bırakır. Peki kapasitansı çok daha büyük yaparsak endüktansın önemli olmadığını söyleyebilir miyiz?

Kısacası: Hayır, bir elektrodinamik cihazı asla tamamen kapasitif veya tamamen endüktif olarak düşünmemeliyiz. Elektrodinamik bir cihazda, yüklerin uzaysal olarak ayrılması nedeniyle her zaman elektrik enerjisi ve yüklerin hareketi nedeniyle manyetik enerji olacaktır. Bazen birinin veya diğerinin göz ardı edilebileceği varsayımsal durumlar oluşturabilsek de, zihinsel bir basitleştirme yaptığımızı her zaman hatırlamamız gerekir.

Dahası, tüm gerçek malzemelerin de bir miktar sınırlı direnci vardır, bu nedenle daha gerçekçi olmak gerekirse, her şeyin bir empedansı olduğunu söylemeliyiz – ve bu, bazen kendimizi daha da fazla belaya soktuğumuz yerdir. Frekans alanı modeliyle uğraşırken, bir elektrikli cihazın empedansı için çok tanıdık bir ifade vardır:

Z = R + j\omega L -j\frac{1}{\omega C}

Direnç, RBu ifadede, hareketli yüklerin, yani akımın kinetik enerjisinin, termal enerjiye nasıl dönüştürüldüğünün bir ölçüsüdür.

Bu denklemin, mühendislik ve fizikte en iyi çalışılan problemlerden biri olan, tek serbestlik dereceli, sönümlü harmonik osilatörle ilgili olduğu hemen fark edilebilir. Bu ifadeden böyle bir osilatörün rezonans frekansı ve kalite faktörünü hesaplayabileceğimizi biliyoruz ve gerçek cihazların temel bir rezonans ve kalite faktörüne sahip olduğunu biliyoruz. Bu bizi ikisini eşitlemeye ve gerçek dünyadaki, sonlu boyutlu bir elektrikli cihazı tek bir dirence, kapasitansa ve endüktansa indirgemeye teşvik eder. Bu kavramsal bir hatadır ve hiçbir zaman geçerli değildir çünkü empedans için yukarıdaki ifade yalnızca sonsuz küçük boyuta sahip bir cihaza uygulanabilir.

Herhangi bir gerçek cihazın sonlu boyutu vardır ve rezonansta çalışırken, yukarıdaki grafiklerden de gördüğümüz gibi, elektrik ve manyetik enerji uzay ve zamanda değişir. Bu nedenle, eşdeğer bir devre modeli, bazen çok daha fazla olsa da, en az üç düğüm, en az üç düğüm gerektirir. Düşüncelerimizi iki kapasitörden oluşan fiziksel modelimize geri çevirirsek ve her kapasitörün plakasının elektrik devresindeki bir düğüm tarafından temsil edildiğini varsayarsak, eşdeğer devre modelinin en az resimde görülen devre kadar karmaşık olması gerektiğini görebiliriz. aşağıda, dört düğümle. Teller boyunca yük ayrımı da olduğundan, tellerin endüktansına paralel olarak küçük bir kapasitansın eklendiğine dikkat edin.

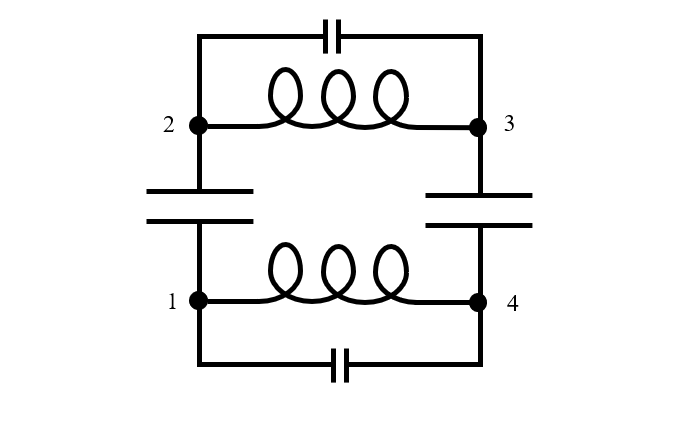
Seri bağlı iki sonlu boyutlu kayıpsız kapasitörün eşdeğer devre modeli.

Bu örnekten, rezonansa yakın geçerli bir eşdeğer devre modeli oluşturmanın hızlı bir şekilde çok karmaşık hale gelebileceğini, fiziksel anlayış, benzer cihazlarla biraz deneyim ve sayısal modelleme gerektirebileceğini umarız.

Orijinal soruya dönersek, kapasitans, endüktans ve hatta direncin kendi başlarına var olmayan kavramlar olduğu, yalnızca birbirleriyle kombinasyon halinde var oldukları ileri sürülebilir. Bazen bir cihazın frekansa bağlı empedansını tek bir direnç, kapasitans ve/veya endüktansa indirgeyebilmemize rağmen, bu tür basitleştirmeler yalnızca cihazın rezonansının altındaki frekanslarda geçerlidir. Bunu akılda tutmak, bu eğlenceli iki kapasitör paradoksundan çok daha sinir bozucu derecede karmaşık gerçek dünya sorunlarına kadar her türlü tuzaktan kaçınmamıza yardımcı olur.

Kapanış Konuşmaları

Rezonansa yakın çalışan bir elektromanyetik cihazın empedansının neden tek bir eşdeğer direnç, kapasitans ve endüktansa ayrıştırılamayacağını anlamak için burada klasik bir düşünce deneyini kullandık. İki kapasitör paradoksu gibi düşünce deneyleri, elektromanyetik anlayışımızı genişletmek ve hesaplamalı modellerimizin sonuçlarını yorumlamak açısından değerlidir.

Daha fazla okuma

Diğer zeka oyunlarını çözmek için modelleme ve simülasyonun nasıl kullanılabileceğini öğrenmekle ilgileniyor musunuz? COMSOL Blogundaki diğer bazı örneklere göz atın:

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.