Optimizasyon Yöntemleri – 3DCAD.news

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.

Süreç oluşturucudaki bağdaştırıcıların sürücüleri olarak mevcut teknikler mükemmeldir. Sayısal yöntemlerde yapılan derinlemesine araştırmaların sonucudur. En öne çıkan teknikler DOE, Optimizasyon, Yaklaşımlar, Altı Sigma'dır. DOE konusunu daha önceki bloglarımızda detaylı olarak ele almıştık. Bu blogda Optimizasyon konusunu derinlemesine inceliyoruz. Süreç oluşturucusu olduğumuzu unutmayalım, dolayısıyla optimizasyon öncelikle geometrik veya fiziksel parametrelere göre parametriktir.

Klasik Optimizasyon Tanımı

Çitlerle çevrili alanda bir yerde bir topunuz var. Bir başlangıç ​​noktanız var. Çiti geçmeden minimum mesafeyi kat ederek topu bulmanız gerekiyor. Yardım için sensörleriniz var. Top, Amaç fonksiyonudur. Çitler kısıtlamalardır. Sensörler kullanılan optimizasyon teknikleridir.

Deney Tasarımı ile Optimizasyon Arasındaki Fark

İkisi arasındaki fark “daha ​​iyi” ile “en iyi” arasındaki farkla aynıdır. Deney Tasarımı, mevcut noktalar kümesinden en uygun tasarım noktasının verimli bir şekilde seçilmesine yönelik bir yöntemdir. Bu set kullanıcı tarafından veya DOE'nin kendisi tarafından tanımlanabilir. Optimizasyon teknikleri tek bir başlangıç ​​tasarım noktasıyla başlar ve en uygun veya en iyi tasarım noktasına ulaşmak için tasarım alanında yinelemeli olarak gezinir. Soruna bağlı olarak DOE, Optimizasyon'un öncüsü olabilir.

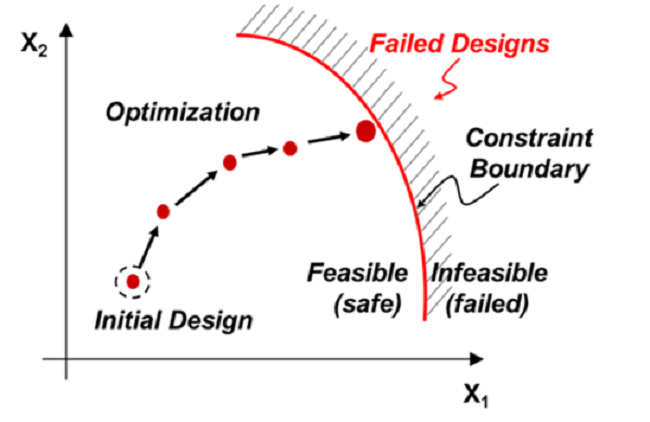
Optimizasyon Tekniklerinin Türleri

Amaç fonksiyonunun nasıl tanımlandığına ve uygun tasarım alanının türüne bağlı olarak bunları kategorize etmenin farklı yöntemleri vardır.

Kısıtlı Teknikler: Çalıştırmak için biri amaç, diğeri kısıtlamalar için ayrı işlevler kullanırlar. Hepimiz mühendislik derslerinde bu tür teknikleri bir düzeyde görmüşüzdür. Bunlar en yaygın olanlardır.

x1>x>x2'de F(x)'i Minimize Et/Maximize Et

Şu şarta tabidir: h(x)>a1; g(x)>a2; f(x)=0 vb.

Kısıtsız Teknikler: Hem amaç hem de kısıtlamalar için yalnızca bir işlev kullanırlar. Kullanıcı yine de Kısıtlamaları Hedeften ayrı olarak tanımlar ancak dahili olarak Kısıtlı problem, Kısıtlamasız bir soruna dönüştürülür.

Farklı tasarım alanı türlerine uygulamaya bağlı olarak optimizasyon yöntemleri Gradyan bazlı, Doğrudan veya Keşifsel olarak sınıflandırılabilir. Aşağıdaki resimlerde gösterilen kısaltmalar, ilgili kategorilerdeki yöntemlerin adlarıdır.

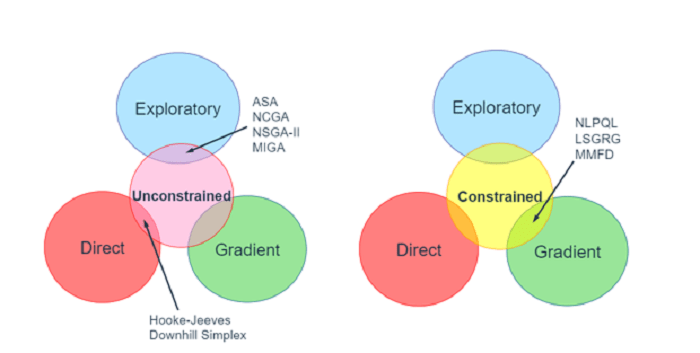
Gradyan Yöntemleri: Bunlar en eskileridir ve sektörde iyi bir şekilde test edilmiştir. Minimum enerji veya maksimum stabilite prensibiyle çalışırlar. Bir topu yavaşça bir vadiye bırakırsınız ve top, yakınındaki en alçak noktaya ulaşana kadar en dik iniş yolu boyunca kayacaktır. Bu yöntemler C0 ve C1 sürekliliğine sahip sürekli tasarım uzayında çalışır. Yerel minimumlara takılıp kalmaları muhtemeldir, bu nedenle başlangıç ​​noktası dikkatle seçilmelidir.

Doğrudan Yöntemler: Doğrudan arama algoritması bir taban noktasıyla başlar. Amaç fonksiyonunun değerinin mevcut değerden daha düşük olduğu bir noktayı bulmak için etrafındaki bir dizi noktayı arar. Algoritma bu noktaya yeni bir temel nokta olarak atlar ve onun etrafında yeni bir dizi nokta arar. Herhangi bir gradyan hesaplaması gerekmediğinden böyle bir yöntemin hesaplama açısından verimli olduğu anlaşılabilir. C0 ve C1 sürekliliği gerekmediğinden daha çok yönlüdür. En yaygın olanları Hooke's-Jeeves ve Downhill Simplex'tir.

Hooke's Jeeves yöntemi seyahat yönünün kaydını tutar. Hareket yönünde daha alçak bir nokta mevcutsa her adımda yönünü değiştirmez.

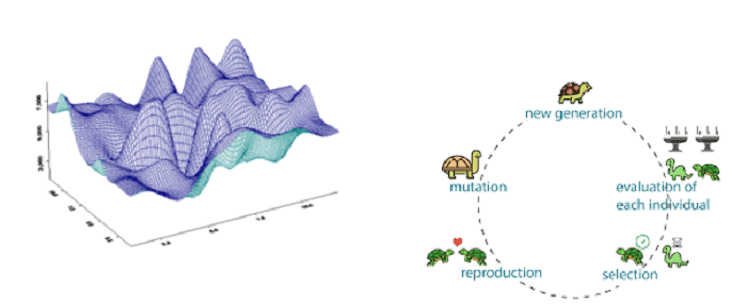
Keşif Yöntemleri: Bu yöntemler, ebeveyn adı verilen bir veri kümesinden çocuk adı verilen başka bir veri kümesi oluşturmak için çaprazlama veya mutasyon tekniklerine dayanmaktadır. Yeni veri seti her mutasyonla birlikte gelişir ve optimum çözüme yaklaşır. Bu, her türlü nesnel fonksiyonla çalışan yüksek doğruluklu bir şemadır: süreksiz, türevlenemeyen, stokastik, karışık tamsayı tipi ve aşağıda gösterildiği gibi birden fazla tepe ve vadi ile oldukça doğrusal olmayan. Ancak hesaplama maliyeti açısından en pahalı optimizasyon şemasıdır. En yaygın yöntemler genetik algoritma, parçacık sürüsü ve uyarlamalı benzetilmiş tavlamadır.

İşaretçi tabanlı yöntemler: Bu, kullanıcının sorunu makul bir doğrulukla çözmek için hangi tür tekniğin en uygun olacağı konusunda hiçbir fikrinin olmadığı durumlarda kullanılan bir karıştır ve eşleştir yaklaşımıdır. İşaretçi yaklaşımı, kullanıcının görselleştirilmesi zor, alışılmadık türde bir tasarım alanıyla karşılaştığında yardımcı olabilir. İşaretçi yöntemi, tercihen her sepetten bir tane olmak üzere en fazla üç optimizasyon şemasından yararlanabilir: degrade, doğrudan ve keşifsel. Optimizasyon ilerledikçe algoritma her yöntemin etkinliğini izler ve verilen soruna en uygun olanı kullanır.

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.