Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Hepimiz katı modellerle çalışırken Kütle Özelliklerine başvurmuşuzdur, özellikle de SOLIDWORKS sertifikaları! Çoğunlukla, yararlı bilgiler bir bakışta kullanılabilir: Yoğunluk, Kütle, Hacim, Yüzey Alanı, vb. Ancak Kütle Özellikleri’nde yer alan bilgilerin geri kalanını, özellikle de en alttaki sayıları nasıl yorumlayabiliriz? Bize tam olarak ne söylüyorlar?
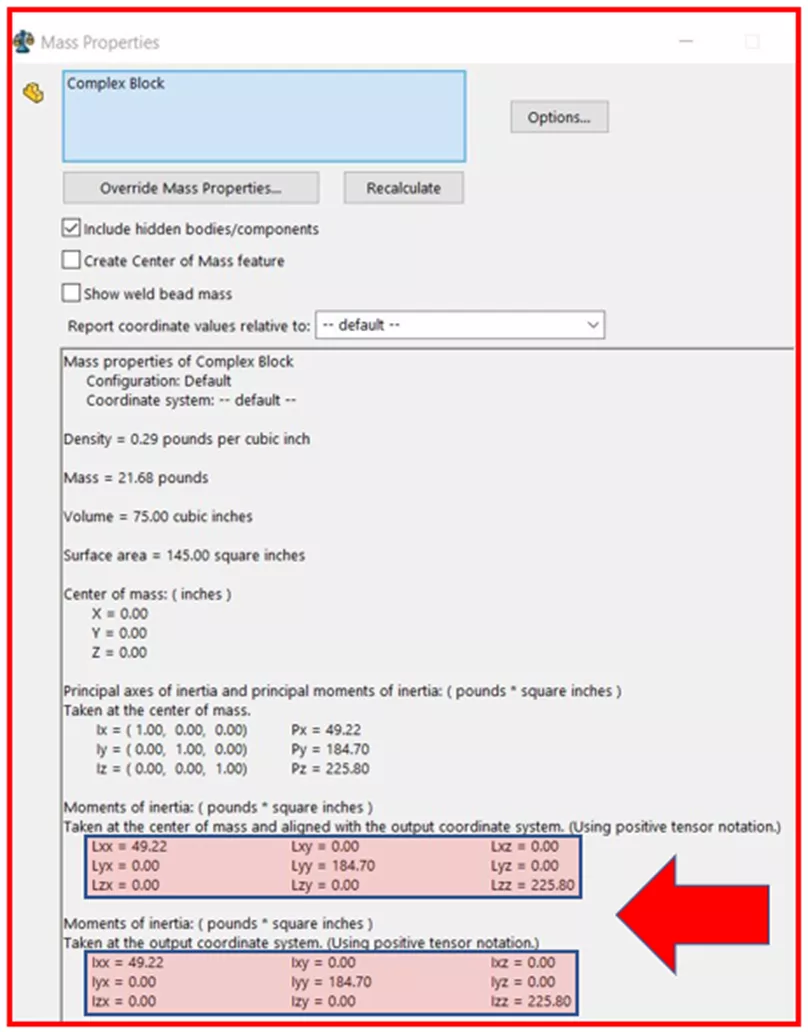
Her şey bir nesnenin kütlesine, şekline ve eksenine bağlı olan Eylemsizlik Momentlerine geri döner. rotasyon.
Her nesnenin bir Kütle Merkezi vardır ve bu noktadan havaya asıldığında mükemmel bir şekilde dengelenir. Aşağıdaki simetrik değerleri alarak karmaşık blok Örnek olarak, kütle merkezinden geçen ana eksenleri görebiliriz.
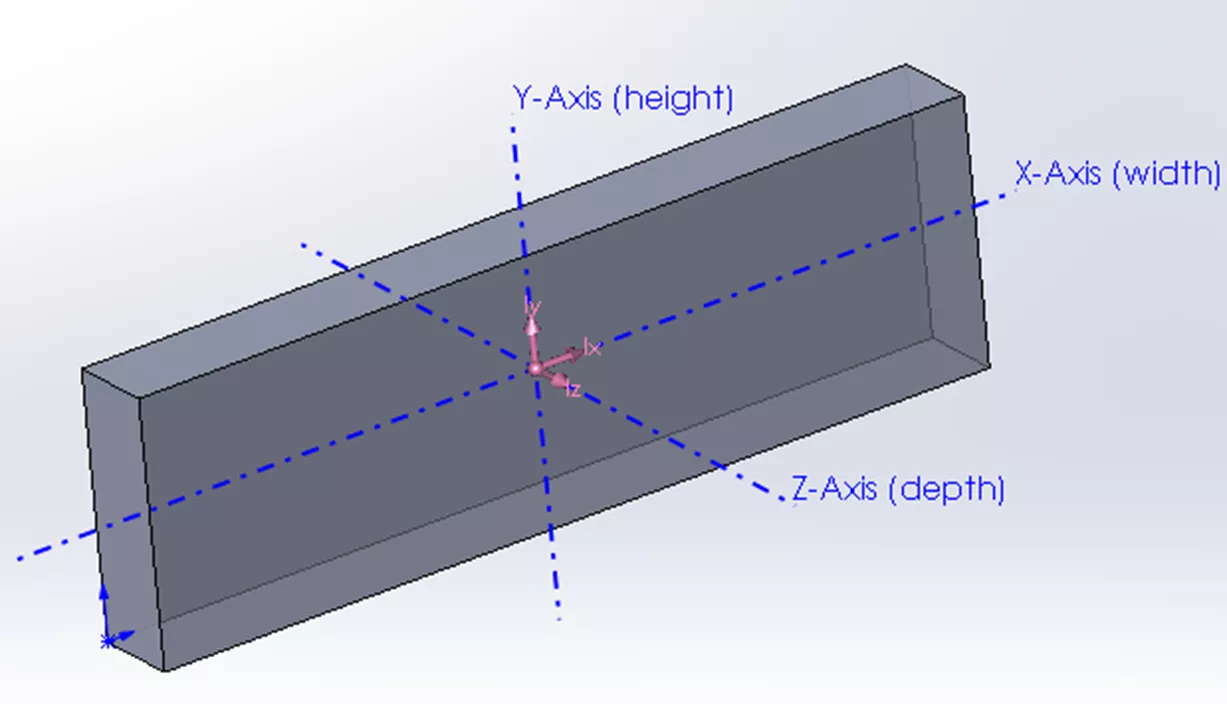
Blok bu eksenlerden herhangi biri etrafında döndürülürse, ML birimlerinde görüntülenen temel Kütle-Moment Atalet değerlerini görürüz2. Bu değerler her bir eksen etrafındaki kütle dağılımını temsil eder.

Kütle-Özellikleri penceresinin altındaki sayı grupları (3×3 matrisler) şunları temsil eder Atalet Tensörleri.

Çok teknik olmadan, bu matrislerin köşegen elemanları her zaman aşağıdakileri temsil eder Kütle Eylemsizlik Momentleri Yerleşik bir koordinat sisteminin ana eksenleri etrafında. Diyagonal olmayan herhangi bir eleman bir Çapraz Ürün MOI. Çapraz ürün MOI aslında sadece nesnenin simetrisinin bir göstergesidir. Eğer sıfır değilse, o zaman eksen dışı bir tork veya ivme bekleyebiliriz ki bu da nesnenin yalpalamasına neden olur; saf bir dönme değil. Bir araba tekerleğini düşünün dengeli sallanmayı önlemek için.
Sadece tek bir düzlemde (XY) simetrik olan bir nesne örneğine bakalım:
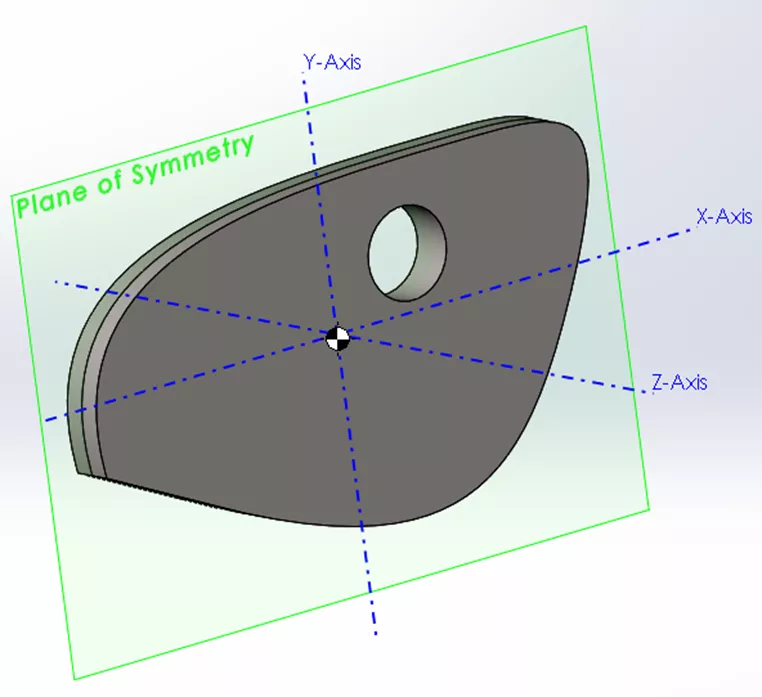
Burada Z eksenini içeren tüm çapraz ürünler için sıfır değerlerini görüyoruz (Z yönünde yalpalama yok). Bunun nedeni, nesnenin kütlesinin bu eksen boyunca simetri düzleminin her iki tarafında eşit olarak dengelenmiş olmasıdır.

Matris gösterimini yorumlamanın bir yolu şudur: eğer bir nesne X ekseni etrafında dönüyorsa, Lxx onun X ekseni etrafında dönmeye ‘karşı’ eylemsizliğidir ve aynı zamanda Lxz onun Z ekseni etrafında dönmeye ‘karşı’ eylemsizliğidir.
Son olarak, muhtemelen Kütle Özelliklerinin de MOI değerlerini verdiğini fark etmişsinizdir. Çıktı Koordinat Sistemi eksenleri. OCS bir parça, montaj vb. başlatılırken varsayılan referans çerçevesidir, bu nedenle konumu bir modelin nasıl oluşturulduğuna bağlıdır.
Aşağıdaki örnekte, blok varsayılan orijinden (ön düzlem) ileriye doğru ekstrüzyonla oluşturulmuştur, bu nedenle OCS sol alt arka köşede yer almaktadır. Çıktı koordinat sisteminin konumunun, bir parça tamamlandıktan sonra bile kolayca değiştirilebileceğini ve bunun Referans Geometri.
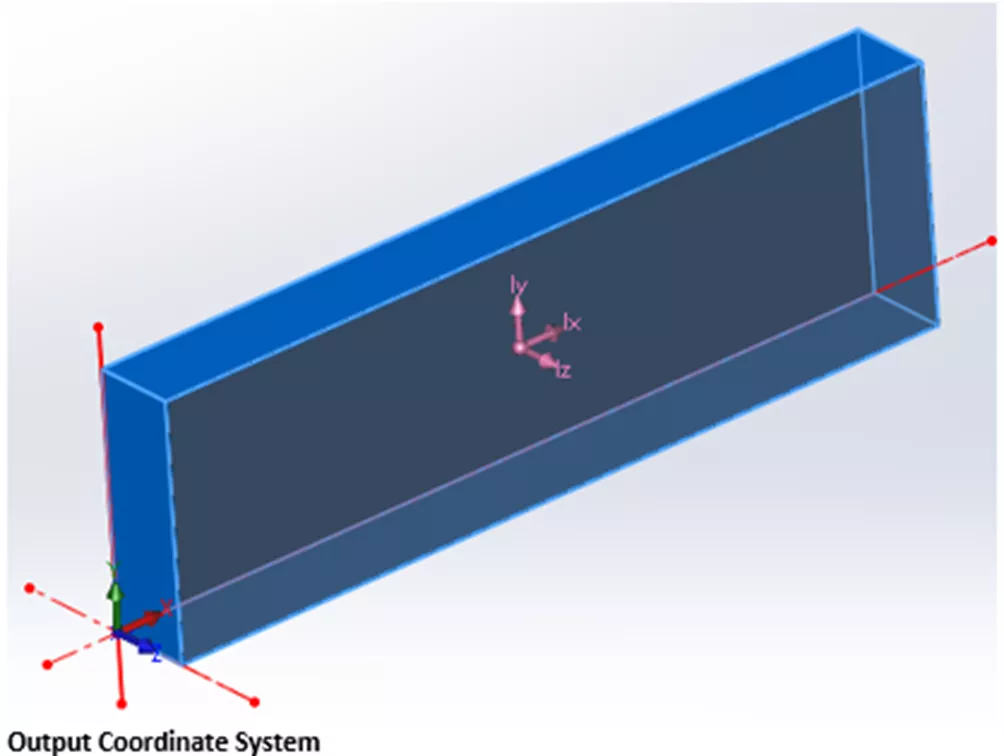
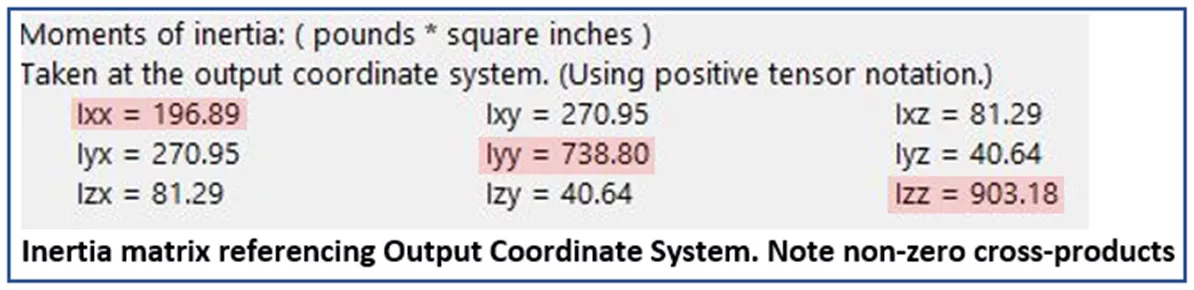
Kütle-Özellikleri’ndeki sayıların alt matrisi, Kütle-Özellikleri’ne referans verilerek hesaplanır. Çıktı Koordinat Sistemi. Bu durumda, örnek modelimizin OCS eksenleri etrafında döndüğünü hayal etmek kolaydır ve beklediğimiz gibi, Eylemsizlik Momentleri çok daha büyüktür. Yine, diyagonal elemanlarda ifade edilen her bir eksenle ilgili MOI’yi görüyoruz, ancak bu sefer, model OCS eksenlerinden herhangi biri hakkında simetrik olmadığı için, tüm çapraz ürünlerde sıfır olmayan değerler görüyoruz.
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.

