Machen Sie eine Schleife für mehrere Punkte

[topogeo]

von einem kreisförmigen rohr habe ich viele punkte auf seinem umfang entdeckt. jetzt muss ich einen einzigen kreis zurückgeben (und dann das zentrum "halb" und seinen radius "halb").
es ist daher ein kreis, der mehrere punkte (von 4 bis 20 variablen) oder besser so nah wie möglich zu diesen punkten durchläuft.
kennen sie einen deckel gegen eine gebühr?

topoge

 

[PlannerRoad]

eine kleine präsentation ist zuerst willkommen:
http://www.cad3d.it/forum1/showthread.php?t=187

 

[Giuseppe Mauro]

ich glaube nicht, dass es existiert. mathematisch können sie einen 3-punkt-kreis erhalten (die 3 punkte eines bogens), aber bereits am 4. punkt, wenn der punkt nicht genau auf dem kreis liegt, wird ein problem.

der rat, den ich ihnen gebe, ist, schrittweise fortzufahren.
erstellen n suchen nach 3 punkten (6 in ihrem fall) und dann erstellen kreise für 3 punkte, die die schnittpunkte der kreise, die sie zuvor erhalten.
so gibt es ihnen weniger fehlerchancen.
zusammengefasst 6 kreise für 3 punkte -> 3 kreise für die 6 kreuzungen (wenn esistino) -> 1 kreis für die neuen schnittpunkte der letzten 3 kreise.
es ist wahr, dass du zwei punkte gesunken hast, aber du warst im durchschnitt auf 18, ich sehe es ziemlich genau.

 

[topogeo]

natürlich kann ein kreis nicht genau für vier oder mehr punkte passieren.
es muss einen abwurf auf jedem geben.
was ich suche, ist eine lüge, die ich diesen "mittleren" kreis geschaffen habe.

ich muss ihnen sagen, dass eine erste lösung, die ich in einer sammlung von diensten angesprochen habe. http://www.dotsoft.com/mwdesign.htm im befehl "kurven" kontrollierte passform.
aber ich hoffe, mehr berichte zu erhalten.

ich werde ihn verärgern.

 

[Antosacca]

sie müssen in drei kreisförmigen sektoren die wolke von punkten (120°), für jeden sektor, um den arithmetischen durchschnitt der ordinate (x1+x2...)/n zu machen; (y1+...)/n: (z1+...)/n, punkte. finden sie die drei punkte mit cooedinate x,y,z. durch die sie ihren umfang bauen. die programme, die ich kenne, mit doppelter klik über dem punkt geben mir die koordinaten des punktes.

 

[AntonioV]

tolle idee, anto', aber unbequem, wenn die wolke von punkten enthält dutzende von punkten, es sei denn, einige "master lisparo" automatisiert nicht das verfahren..

:

 

[Antosacca]

einfacher, aber weniger genau: immer drei sektoren und bauen eine oberfläche unter den extremsten punkten, schnappen sie auf baricentro oberflächen und machen sie ihren schönen umfang, (auch kreis) mit den drei punkten.

 

[AntonioV]

noch genauer:

1] ich mache einen punkt jedes der drei sektoren

2] ich gebiete die einzelnen dreiecke und schließe sie in einem einzigen bereich

3] _massprop darauf, und ich habe das genaue zentrum (und nicht annähernd)

4] hoop für 3 baricentres

:

 

[Fulvio Romano]

diese methode der sektoren ist falsch. zumindest, wenn ich verstehe, was wir suchen.
ich glaube, ich verstehe, dass wir auf der suche nach umfang sind, der seinen abstand von verschiedenen punkten minimiert. datum der verteilung [più di due] punkte gibt es nur einen umfang mit dieser eigenschaft.

wenn sie die sektoren ändern, auch wenn sie nur diese 120° drehen, ist es ziemlich einfach zu zeigen, dass sie immer verschiedene umfange finden, und dies ist genug, um zu beweisen, dass die methode falsch ist, auch wenn sie viel auf die genaue antwort zu nähern.

ich weiß nichts über lisp, vielleicht kann ich einen einfachen metallisierungsalgorithmus schreiben, den jemand in...

 

[AntonioV]

diese methode der sektoren ist falsch

ich würde sagen, dass der ansatz von antoxac die weniger "falsch" unter allen möglichen empirischen methoden.

:

 

[Antosacca]

wenn sie die sektoren ändern, auch nur durch drehen dieser 120°,

:smile: die gleichung, die einen solchen umfang löst (mehr punkte und vielleicht nur wenige backen im gleichen) ist unlösbar, bereits oben erwähnt.
daher geht man in der nähe, die durch antoniov beschrieben wird, das ist der schwerpunkt ist der einzige, der sich der lösung rüttelhaft nähert.
ps rotieren das stativ erzeugt nur eine verschiebung in der mitte des umfangs, die nicht gegen die auflösung des problems ist.:36_6_6:
mit liebe, antoxac.

 

[AntonioV]

drehen des stativs bewirkt nur eine verschiebung in der mitte des umfangs

wahr, aber da die wolke der punkte noch vorhanden ist, wird jede verschiebung im zentrum eine neue umfang, deutlich vom vorherigen: mit anderen worten, jedes neue stativ schafft einen neuen platz von punkten mit einem minimalen mittleren abstand von der wolke.

um den fehler zu minimieren, sollten sie das dreifache von 1 grad wegdrehen und so 60 umfänge erstellen.

schließlich sollten wir unter ihnen die 60 zentren durch farbstoff verbinden, von denen aus den schwerpunkt zu extrahieren, der das zentrum des letzten "area" umfanges sein wird.

:

 

[Fulvio Romano]

:smile: die gleichung, die einen solchen umfang löst (mehr punkte und vielleicht nur wenige backen im gleichen) ist unlösbar, bereits oben erwähnt.

was?
eine gleichung ist nur unlösbar, wenn schlecht platziert.
wenn das problem eine lösung zugibt, gibt es ein mathematisches modell, das es findet. nicht in der lage, das modell zu lösen, bedeutet einfach, es falsch zu bauen.

um den fehler zu minimieren, sollten sie das dreifache von 1 grad wegdrehen und so 60 umfänge erstellen.

schließlich sollten wir unter ihnen die 60 zentren durch farbstoff verbinden, von denen aus den schwerpunkt zu extrahieren, der das zentrum des letzten "area" umfanges sein wird.
:

wie sagen sie, dass die lösung auf diese weise richtig ist?

ich versuchte jedoch, das problem anzusprechen, und es ist eigentlich nicht einfach.
ich versuchte die methode von lyapunov*, aber die formeln wachsen. wenn ich zeit finde, weiterzugehen, und ich kann eine lösung finden, kann ich es posten, genauso wie mentale übung, denn dann weiß ich nicht, ob es möglich sein wird, es in lisp zu übersetzen.

(*)
stellen sie sich vor, dass jeder punkt eine energie aus dem abstand vom umfang hat. wenn ich mit dem lyapunov-theorem einen punkt der stabilität des systems finden kann, wird es mit dem umfang zusammenfallen, den wir suchen. oder?

 

[Antosacca]

stellen sie sich vor, dass jeder punkt eine energie aus dem abstand vom umfang hat. wenn ich mit dem lyapunov-theorem einen punkt der stabilität des systems finden kann, wird es mit dem umfang zusammenfallen, den wir suchen. oder?

gefunden das resultierende, was ein träger ist, finden in der tat das zentrum der punkte massen (datenpunkte), aber welchen radius verwenden sie? risiko um ihr zentrum mit einem gebrochenen.
die punkte eines umfangs skalierbar sind und als alle punkte definiert sind, die von einem punkt, der den mittelpunkt des umfangs nennt, gleich groß sind. wir verstehen das problem nicht.
die auflösung sollte in der statistik gesucht werden und die genauigkeit hängt von der verwendeten methode ab, sie können die extremsten punkte und / oder die meisten internen, etc. löschen.
die definition des umfangs, die grundlage der forschung, ist klar.
:3513::3513::3513:

 

[Fulvio Romano]

gefunden das resultierende, was ein träger ist, finden in der tat das zentrum der punkte massen (datenpunkte), aber welchen radius verwenden sie? risiko um ihr zentrum mit einem gebrochenen.
die punkte eines umfangs skalierbar sind und als alle punkte definiert sind, die von einem punkt, der den mittelpunkt des umfangs nennt, gleich groß sind. wir verstehen das problem nicht.
die auflösung sollte in der statistik gesucht werden und die genauigkeit hängt von der verwendeten methode ab, sie können die extremsten punkte und / oder die meisten internen, etc. löschen.
die definition des umfangs, die grundlage der forschung, ist klar.
:3513::3513::3513:

vergib mir, aber abgesehen davon gibt es in meiner methode kein ergebnis, aber was meinst du mit "präzision des ergebnisses"?
außerdem ist die mitte der punkte nicht die mitte des umfangs. aus keinem grund in der welt kann sein.
stellen sie sich vor, eine wolke von punkten zu haben und den umfang zu kennen, der sie annähert. fügen sie nun nach oben links einige punkte hinzu, die gleichen abstand vom umfang haben.
ändert sich der umfang? sicherlich nicht, aber der schwerpunkt bewegt sich nach oben links. die mitte und die mitte des umfangs sind auf verschiedenen planeten.

 

[AntonioV]

wie sagen sie, dass die lösung auf diese weise richtig ist?

aber das habe ich überhaupt nicht gesagt: ich sprach von "minimieren" des fehlers, auf der suche nach einer akzeptablen annäherung.

darüber hinaus ist dies keine frage der lisp, in der tat, dass die diskussion von einem benutzer von pro-e oder medusa gestartet wurde.

es ist ein faszinierendes problem, weil es nicht "kanonisch" ist. ich und meine namen versuchen geometrisch, sie mit lyapunov, aber in ordnung, glauben sie mir.

:

 

[Giuseppe Mauro]

mah, vielleicht werde ich zu viele mentale zuhälter bekommen, aber ich denke, es ist falsch, das problem anzusprechen.

topogee sagte etwas wesentliches und was er fand 18 punkte auf einem kreis.
erkannte 18 punkte "ad canem penis" nicht und will einen perfekten kreis herausnehmen.
nun, es wird angenommen, wenn sie kein werkzeug haben, das mit einer sarta fettuccia vergleichbar ist (was sehr nützlich ist und dann werden wir sehen, warum), dass die entdeckten punkte liegen auf der umfang, mit einer abweichung, die vom fehler des instruments abgeleitet ist.
wie viel fehler wollen wir einem erkennungstool geben? wenn es topographische (wie ich mir aus dem spitz vorstellen) werden wir in der größenordnung von 1 pro tausend sein? mein lasermessgerät aus einer toleranz von 3mm von 100m (ich glaube nicht, dass ich es sehe, aber das ist der angegebene wert)
dann schuf ich mich in autocad ein 1000 radius kreis unterteilt in 18 punkte und randomisiert mit maximaler entfernung 50, dann mit einem fehler (gedreht) von gut 5% (leer zu sagen, dass das instrument 5cm jeden meter verlieren sollte, außer meter nach maß).
ich schuf eine spline, die alle punkte durchläuft, die sich ergeben, geschlossen, und von diesem eine region. ich forderte den massenprospekt der region i, der 2 grunddaten erhalten hat.
eins ist das herzstück und eins ist der bereich der sym-kreisförmigen figur.
ich teile das gebiet für faul und mache es zur quadratwurzel. ich finde den radius der entsprechenden fläche. ich brauche das zentrum meines kreises... und woila.

ausgehend von den grunddaten, 1000 kreis mit einem monströsen fehler von 5%, fand ich mich mit einem radius kreis 998.129 (so weniger als 2 pro tausend fehler) und aus dem realen zentrum von 2,54 (2,5 pro tausend fehler)

zurück zum zähler von schneider (oder sogar bindella ab 20m). als steuerelement genügt es, ihn entlang des kreises zu wickeln (weil "topogee immer ein zylindrisches objekt hat, das gefunden hat, also vorhanden), um mit allen grenzen der bindella einen umfang zu erhalten. teilt den für 2pi erhält seinen radius, der mit der methode des bereichs vergleichen kann.

 

[Antosacca]

aber was meinst du mit "präzision des ergebnisses"?

ich bin die unbestimmtheit der lösung, also glaube ich, dass wir zu einer durchschnittlichen lösung kommen müssen.

vorstellen, dass jeder punkt energie hat

physikalisches zentrum nicht mehr geometrische.
aber wir verlängern die diskussion nicht zu viel, antoniov und ich haben eine lösung vorgeschlagen, roman datti zu tun und "facci" sti conti, um zu ihrer lösung zu gelangen, die sie zuvor blind gemacht hatten.
ich würde ihnen gerne einen grund geben.
ich entschuldige mich für zu viele facine, wie eine verordnung, die ich jetzt nur gelesen habe.

 

[Antosacca]

große mauro und dies ist eine weitere lösung.

 

[Fulvio Romano]

ich spreche eigentlich so viel, aber ich habe noch nichts geschrieben, stattdessen haben sie etwas geschrieben.
ich möchte jedoch einige punkte machen. weil ich nicht verstanden habe, welche präzision sie dient, aber die bisher vorgeschlagenen methoden bringen einen systematischen fehler, den ich nicht weiß, ob er toleriert werden kann.

1. was juseppe mauro sagt, ist nur, wenn zwei grundlegende annahmen zufrieden sind. das heißt, dass die punkte gleich verteilt sind und einen durchschnittlichen fehler haben nichts (was nicht durch alle instrumente garantiert wird).

2. die tatsache, dass er eine energie hat, ist absolut nichts mit dem schwerpunkt zu tun. die methode von lyapunov braucht eine energietypische objektive funktion zu optimieren, und bis jetzt versuche ich, den abstand von punkten vom umfang zu verwenden, nicht von der mitte, daher hat es nichts mit der mitte zu tun.

wir beobachten die veröffentlichten bilder, die die situation klären sollten und erklären, warum die vorgeschlagenen methoden jetzt falsch sind. sie nehmen es nicht, selbst wenn ich nicht in der lage gewesen, eine lösung zu finden, bedeutet es nicht, dass, wenn ich einen fehler in ihrem finde, ich habe nicht das recht, es zu präsentieren. wenn ich ein auto gegen meine hand sehe, lasse ich den fahrer wissen, ob ich keinen führerschein habe, oder? :finger:

bild 1
ich habe eine verdickung von punkten oben rechts, aber diese punkte identifizieren mich immer den gleichen umfang, ich habe das instrument einfach für mehr zeit in diesem bereich gehalten. wenn der algorithmus gut funktioniert, sollte ich immer den gleichen umfang bekommen, stattdessen scheint es offensichtlich, dass die mitte der punkte (mit denen sie versuchen, die mitte des umfangs zu finden) massiv nach oben links bewegt.

bild 2
ich habe keine punkte auf der unteren hälfte des umfangs. die daten zur lösung des problems gibt es, aber keine bisher vorgeschlagene methode kann den umfang finden. oder?

bild 3
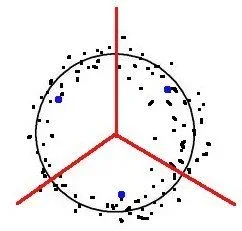
die intelligenteste methode ist, die cloud in drei sektoren zu teilen. das zentrum jedes sektors (blau markiert), liegt aber nicht am umfang. es scheint mir ganz offensichtlich, dass es näher an der mitte ist, wie die verteilung der punkte gemacht wird. daher wird dieses verfahren systematisch kleinere umfangs erzeugen als die richtigen.

kurz gesagt, ich denke, auch wenn wir in den toleranzen des problems sind, sind wir nicht wirklich da. denkst du?